for文で繰返し計算を行い、if文により必要なデータを宝箱に保管しておくテクニック記事の追加例題です。次のステップに進もうかと思いましたが、もう少し、例題を解くことにしました。また、この記事では絶対値を求める関数abs()を使って、誤差を判定します。
なお、以下の記事の続編となります。
Python♪基本:大切なものは「宝箱」に保管するテクニック
ゆうちゃんは、前回の記事では、最後の例題で少し苦戦していました。考え方は合っているのに、X座標とY座標を逆に考えてしまい、そのミスを見つけきれませんでした。わからないというよりは、バグを消すのに慣れていないのだと思います。
ゆうちゃんは、すぐにパッとひらめくし、勘がするどい。でも、しつこく粘るタイプではありません。すぐにヒントを聞きたいのに、悔しいというジレンマがあり、ヒントを聞くたびに機嫌が悪くなります。
ゆーちゃん♪ 地味なバグ消し作業を黙々とこなすには、まだ、幼いのかもね。自力で解決する練習が必要ね。
ということで、前よりも少しだけ難しい例題を1問だけ追加します。ゆうちゃんの嫌い(好き?)なヒントを7つも用意しました。見たい、見たくないというジレンマの中で、いくつまでヒントに頼ってしまうのでしょうか。どんな、展開になるのか楽しみ~。
ゆうちゃん「きたよ~♪」
わたし「ゆうちゃん、ゆうちゃん、すごく、難しい問題用意したんだけど解く?」
ゆうちゃん「すごく、難しいなら、嫌。」
わたし「でも、ヒントが7つもあって、ゆうちゃんなら、全部見なくてもできると思うんだけど。」
ゆうちゃん「今日は、僕を挑発する作戦だね。その挑発にのってあげるよ。ヒントなんかいらない。」
今日は、ご機嫌がよろしいみたい。(しめしめ)
0.ゆうちゃんとPythonシリーズ
この記事は「ゆうちゃんとPythonシリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。
なお、それぞれの記事は、シリーズの中でそれまでに習った文法を使ってサンプルコードを考えています。実際には、もっと、効率のよい書き方があるかもしれませんが、ご了承ください。
1.絶対値を求めるabs()
さて、例題を解く前に、今日はabs()の使い方を覚えましょう。
さて、いきなりですが、35, 32, 36の中で、最も30に近いものはどれでしょうか。これは、人が見れば一瞬で32とわかります。そして、これを判定するならば、例えば以下のように30との差を求め、差がが最も小さい32が答であると言えます。
35 - 30 = 5
32 - 30 = 2
36 - 30 = 6では、24, 35, 32の中で、最も30に近いものはどれでしょうか。これも、一瞬で32とわかりますが、先ほどと同じように差に注目すると、- 6が一番小さい値となり、答が24になってしまいます。
24 - 30 = - 6
35 - 30 = 5
32 - 30 = 2つまり、誤差を比較するには、30との「差」ではなく、「差の絶対値」を求める必要があります。
Pythonでは絶対値を求める関数としてabs()という関数があります。()の中の数字の絶対値を求める関数です。最初からPythonの機能として組み込まれた「組み込み関数」ですので、特にライブラリーをimportする必要はありません。
以下のように、abs()を使い、print()で出力してみます。差の絶対値を求めれば、32が最も30に近いことがわかります。 あえて、テクニックと言うほどのことではありませんが、誤差を判定したいことはよくあると思いますので、そんなときには組み込み関数のabs()を使ってください。
#コード01
print(abs(24 - 30))
print(abs(35 - 30))
print(abs(32 - 30))#出力01
6
5
2さて、これで、新しい例題を解くための準備は完了です。
2.追加例題の設定
追加例題の設定は前回と同じです。
あるところに研究熱心な愛のキューピットがおりました。射程距離が短い弓矢では、なかなか、愛の矢が当たらないので、愛の大砲を発明しました。この大砲は空気抵抗などは受けない愛の砲弾を撃つことができ、その威力は絶大です。
大砲は火薬の量で、砲弾の最初の速度を変えることはできますが、発射角は45度固定です。以下の図のように、城壁の上からターゲットに向けて発射されます。
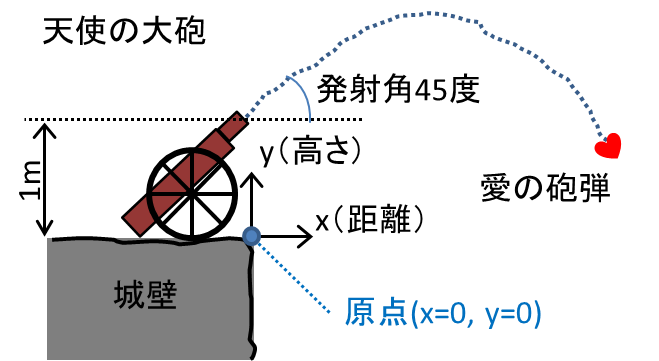
この場合の弾道は、原点(x=0, y=0)を城壁の角の部分とすると、水平距離xと高さyの関係を以下の式であらわすことができます。大砲の筒先までの高さが1mなので、式の最後が「+1」になっています。
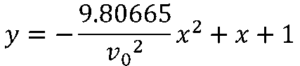
x, yの単位は(m)、砲弾が大砲を飛び出すときの初速(v0)の単位は(m/秒)です。
3.例題(命中させるための初速を知りたい)
天使は城壁の高さ(h_wall)が5mのところに愛の大砲を設置しました。城壁から5m下の標的に命中させるためには、火薬の量により砲弾の初速(v0)を変えて飛距離を調整します。
さて、50m先にあるターゲットの足元に愛の大砲を命中させるための、砲弾の初速(v0)を求めましょう。なお、現在の天使界の技術では、初速は最大25(m/秒)までしかでません。
様々な解答が考えられますが、この記事は Python♪基本:大切なものは「宝箱」に保管するテクニック の追加例題であり、前回記事の例題4の解答を参考にしてください。また、グラフを表示する必要はありません。
4.ヒント
さて、ゆうちゃん♪ たくさん、ヒントを用意したよ!いかが?
(1) ヒント1
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
与えられた(1)式において、この問題ではターゲットまでの距離xは50mと決まっています。したがって、(1)式のxは消え、yとv0の関係を表す(2)式になります。つまり、(2)式のv0を色々かえて、答の条件に合うyの値を考えればよいのです。
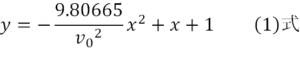
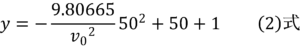
(2) ヒント2
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
50mに到達したときに、yの値がどんな値になっていれば、命中するのでしょうか。
(3) ヒント3
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
50mに達したときに、もし、y=-3だとすると、50mの時にターゲットの頭上を越えてしまうことになると思います。 一方、y=-7であったとすれば、それは地面の高さy=-5よりも下の座標ですから、この場合は、ターゲットより手前で既に着弾してしまっていることになります。
(4) ヒント4
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
城壁の高さが5mということは、水平距離が50mに到達したときに、yの値が-5mになっていれば、命中します。では、yの値が-5に近いとは、どのように表現すればよいでしょうか。
(5) ヒント5
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
誤差は、差の絶対値を求めればよかったですね。yの値が-5に近いということは abs(y-(-5))が誤差です。注意しなければならないのは、abs(y-5)ではありません。これではy=5になってしまいます。
(6) ヒント6
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
宝箱に保存する値をなににすればよいのでしょうか。ターゲットに命中するときの弾丸の初速v0を求めるのですから、まず、v0を宝箱に保存しなければ、答えは求まりません。次に、v0がどのくらい求めたい答えに近いかを示す数値も宝箱に保存しなければなりません。なぜなら、今のデータと新しいデータの比較ができないからです。つまり、「v0」と「誤差abs(y-(-5))」を宝箱に保存すればよいのです。
(7) ヒント7
ヒントの表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
私の解答例では、入出力の変数を以下のように設定しました。
(1)入力
v0_min:初速の最小値(m/秒)
v0_max:初速の最大値(m/秒)
h_wall:城壁の高さ(m)
x_target:ターゲットまでの水平距離(m)
n_cal_i:繰り返し計算回数。(水平距離をランダムに与える)(回)
(2)出力
v0_hit:ターゲットに命中させるために必要な弾丸の初速(m)
y_gosa_min:y座標(高さ方向の位置)の誤差(m)5. 解答例
理論値による砲弾の初速は20.92359613 (m/秒) です。この答に近い値になれば正解です。答が合わない場合は解答例を開かず、考え直しましょう。10000回繰り返し計算することで、だいたい20.92ぐらいまでは合うのではないかと思います。
解答の表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
今までの例題は、求めたい対象と、x座標かy座標を宝箱に保管すればよかったですが、このコードではyから計算した誤差を宝箱に保管しています。そこが、問題を少しだけ難しくしています。for文で何度も計算を繰り返し、よりよい答を探し続けるためには、何を残さなければならないのかを考えなければなりません。
#コード01
'''天使の大砲のターゲットに命中させる初速算定プログラム
発射角が45度、城壁の高さが5mのとき、50m先のターゲットに
命中させるために必要な弾丸の初速を求める。
初速は0.0m/秒~25.0m/秒までの範囲で設定できる。
(1)入力
v0_min:初速の最小値(m/秒)
v0_max:初速の最大値(m/秒)
h_wall:城壁の高さ(m)
x_target:ターゲットまでの水平距離(m)
n_cal_i:繰り返し計算回数。(水平距離をランダムに与える)(回)
(2)出力
v0_hit:ターゲットに命中させるために必要な弾丸の初速(m)
y_gosa_min:y座標(高さ方向の位置)の誤差(m)
'''
import random
#入力
v0_min = 0.0
v0_max = 25.0
h_wall = 5.0
x_target = 50
n_cal_i = 10000
#計算
v0 = random.uniform(v0_min, v0_max)
y = - 9.80665 / (v0 ** 2) * (x_target ** 2) + x_target + 1
v_hit = v0
y_gosa_min = abs(y-(-h_wall))
for i in range(n_cal_i):
v0 = random.uniform(v0_min, v0_max)
y = - 9.80665 / (v0 ** 2) * (x_target ** 2) + x_target + 1
y_gosa = abs(y-(-h_wall))
if (y_gosa_min > y_gosa):
v0_hit = v0
y_gosa_min = y_gosa
#出力
print('必要な初速:', v0_hit)
print('誤差の参考値:y_gosa_min=', y_gosa_min)
以下、理論値と5回分の出力結果です。
初速、理論値:20.9235961297288
<以下、5回分の出力>
必要な初速: 20.923414346839746
誤差の参考値:y_gosa_min= 0.0009730616463343722
必要な初速: 20.920620627377946
誤差の参考値:y_gosa_min= 0.015930691944880948
必要な初速: 20.925312052270716
誤差の参考値:y_gosa_min= 0.009183874748821097
必要な初速: 20.924490144563133
誤差の参考値:y_gosa_min= 0.004785183376078805
必要な初速: 20.923436892080673
誤差の参考値:y_gosa_min= 0.00085237834213813816.余談
ゆうちゃんには、15分ぐらい考えてもらった後に、ヒント1だけ聞いてもらいました。
ゆうちゃん「今日は、ヒントを見ないのが大切なんだよね?」「僕、ヒントいらない。」
(少しムキになって、ほっぺが、少し赤くなっているのがかわいい。)
わたし「なにいってるの。せっかく、たくさんヒントを用意したんだから、ちょっとぐらいヒントを見てくれた方が楽しいよ。」「ということで、ヒントはね・・・」
ゆうちゃん「わ~。わ~。わ~。」(耳を塞いで聞かないモード)
でも、聞かないモードでも、少しだけ、聞こえてたみたい。
結局、やっぱり、バグ消しが苦手のようで、 ティータイムを何回かはさんで、悔しそうに例題を家に持って帰りました。ちょっと、かわいそうだったかな・・・。
そして、次の週
「きたよ~♪シュークリームもあるよ~。」ゆうちゃんが、やってきました。あの声の感じは出来たみたいね。お尻についてた卵の殻が少しとれたのかしら。
私が実際に購入した教材のご紹介
以下、私が実際に購入したPythonの教材をまとめてみました。 Pythonを学習する上で、少しでもお役に立つことができればうれしいです。
・Python♪私が購入したPythonの書籍のレビュー
・UdemyのPythonの動画講座を書籍を買う感覚で購入してみた
その他
液晶ペンタブレットを買いました
(1) モバイルディスプレイを買うつもりだったのに激安ペンタブレット購入
以下、私が光回線を導入した時の記事一覧です。
(1) 2020年「光回線は値段で選ぶ」では後悔する ←宅内工事の状況も説明しています。
(2) NURO光の開通までWiFiルーターを格安レンタルできる
(3) NURO光の屋外工事の状況をご紹介。その日に開通!
(4) 光回線開通!実測するとNURO光はやっぱり速かった
(5) ネット上のNURO光紹介特典は個人情報がもれないの?


