三角関数の-θ、θ±360°、θ±180°、θ±90°、の符号

三角関数の -θ、θ±360°、360°±θ、θ±180°、180°±θ、θ±90°、90°±θ、の符号は、一見難しそうに見えますが整理して覚えると簡単です。語呂合わせや加法定理を使わなくても覚えられるので、しっかりマスターしてください。

また、三角関数の計算では「え～っと・・・」と公式を思い出しながら解くようでは間違えてしまいます。覚える数が多いので大変に感じるかもしれませんが、以下の覚え方をマスターすれば公式の符号が感覚的にわかるようになると思います。

なお、参考書では180°±θ、 90°± θが公式として記述されているものも多いですが、180°±θ、 90°± θよりもθ±180°、θ±90°から優先して覚える方が覚えやすいし、使いやすいと思います。

1. 公式一覧と覚え方
2. まとめ
3. おまけA: 180°-θの符号をグラフから読み解く
4. おまけB: 90°-θの符号をグラフから読み解く
5. おまけC: θ±90°、90°±θの語呂合わせ
6. あとがき

1. 公式一覧と覚え方

三角比の -θ、θ±360°、360°±θ、θ±180°、180°±θ、θ±90°、90±θ°、の公式の一覧と覚え方を説明します。

なお、公式を覚える前にsin,cos,tanのグラフを眺めて、以下の内容をイメージできるようにしてください。これがイメージできれば実は公式として覚えなくても分かるようになります。

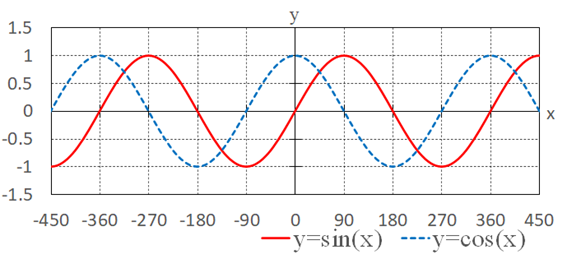
sin,cosの周期は360°、tanの周期は180°。
cosはy軸に関して線対称。（y軸で折り返しても同じ形になる。）
sin,tanは原点に関して点対称。（y軸で折り返し、更にθ軸で折り返すと同じ形になる。）
sin(x), tan(x)は原点付近で右上がり
cos(0)=1, sin(0)=0, tan(0)=0
sinはcosよりも位相が90°進んでいる。（sinはcosよりもグラフの右側に90°進んでいる。）
sin,cosは位相が±180°(周期の半分)変化するとyの符号が反転する。大きさは同じ。
tanは位相が±90°(周期の半分)変化するとyの符号が反転する。大きさが同じとは限らない。

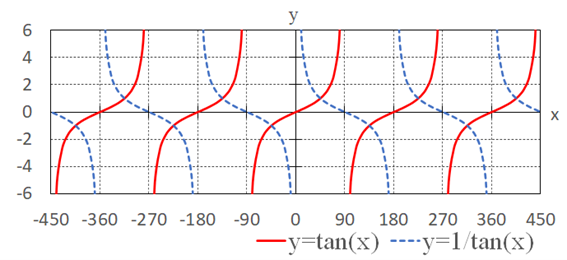
1/tan(x)については、以下の性質を覚えておきましょう。

tan(x)と1/tan(x)の符号は同じ
tan(x)=0の位置が、1/tan(x)の漸近線の位置となる。
1/tan(x)=0の位置が、tan(x)の漸近線の位置となる。
tan(x)と1/tan(x)はx=45°の直線に関して線対称
tan(x)を左に90°ずらし、x軸に関して対称移動すると1/tan(x)と一致する。

(1) \(\small -\theta\)

\(\small y=\cos (x)\)はｙ軸に対して対称なので、角度の符号が反対になっても符号は変わりません。

一方、 \(\small y=\sin (x)\) 、\(\small y=\tan (x)\)は原点に関して点対称であり、y軸に対して対称なグラフを、更にx軸に対して対称にしたグラフです。つまり、 \(\small x\) に\(\small -\theta\)を代入すると符号がマイナスになります。

\(\small \sin (-\theta)=-\sin \theta\hspace{50pt} (1a)\)
\(\small \cos (-\theta)=\cos\theta\hspace{57pt}(1b)\)
\(\small \tan (-\theta)=-\tan \theta\hspace{46pt}(1c)\)

なお、以下の内容については復習しておきましょう。

y=f(x)→y=f(-x)とすると、y軸に対して対称なグラフとなります。
y=f(x)→-y=f(x)では、x軸に対して対称なグラフになります。
y=f(x)→-y=f(-x)では、y軸に対して対称なグラフを、更にx軸に対して対称にしたグラフとなります。

(2) \(\small \theta±360^{\circ} ,\hspace{8pt} 360^{\circ}±\theta\)

\( \small \sin \), \(\small \cos \)は、周期が\(\small 360^{\circ}\)なので符号は変わりません。
また、\( \small \tan \) は周期が \(\small 180^{\circ}\)なので、 \(\small 360^{\circ}\) は \(\small 180^{\circ}\) の倍数であり、符号は変わりません。

\( \small \sin \left(\theta+360^{\circ}\right)=\sin \theta \hspace{37pt} (2a) \)
\( \small \cos \left(\theta+360^{\circ}\right)=\cos \theta \hspace{35pt} (2b) \)
\( \small \tan \left(\theta+360^{\circ}\right)=\tan \theta \hspace{33pt} (2c) \)

\( \small \sin \left(\theta-360^{\circ}\right) \) \(\small =\sin \theta \hspace{37pt} (2d) \)
\( \small \cos \left(\theta-360^{\circ}\right) \) \(\small =\cos \theta \hspace{35pt} (2e) \)
\( \small \tan \left(\theta-360^{\circ}\right) \) \(\small =\tan \theta \hspace{33pt} (2f) \)

\( \small (2g)(2h)(2i)\)は \( \small (2a)(2b)(2c)\) と同じです。
\( \small \sin \left(360^{\circ}+\theta\right)=\sin \theta \hspace{37pt} (2g) \)
\( \small \cos \left(360^{\circ}+\theta\right)=\cos \theta \hspace{35pt} (2h) \)
\( \small \tan \left(360^{\circ}+\theta\right)=\tan \theta \hspace{33pt} (2i) \)

\( \small (2j)(2k)(2l)\)は\(\small(2d)(2e)(2f)\) に対して角度の正負が反対なので、 \( \small (2d)(2e)(2f)\)に対して \(\small\cos\)は符号が変わらず、\(\small\sin\)と\( \small \tan\)は符号が変わる。※ \(\small\cos\) だけ符号が変わらないのは\( \small (1a)(1b)(1c)\) を参照。
\( \small \sin \left(360^{\circ}-\theta\right)\) \(\small =-\sin \theta \hspace{30pt} (2j) \)
\( \small \cos \left(360^{\circ}-\theta\right) \) \(\small =\cos \theta \hspace{35pt} (2k) \)
\( \small \tan \left(360^{\circ}-\theta\right) \) \(\small =-\tan \theta \hspace{27pt} (2l) \)

（参考） sin(360°-θ) = sin(-(θ-360°)) ＝-sin(θ-360°) = -sin(θ)

(3) \(\small\theta±180^{\circ} ,\hspace{8pt} 180^{\circ}±\theta\)

\( \small \sin \), \(\small \cos \)は、周期が\(\small 360^{\circ}\)なので、周期の半分である\(\small 180^{\circ}\)では符号が変わります。
一方、\( \small \tan \) は、周期が \(\small 180^{\circ}\)なので符号は変わりません。

\( \small \sin \left(\theta+180^{\circ}\right)=-\sin \theta\hspace{29pt} (3a)\)
\( \small \cos \left(\theta+180^{\circ}\right)=-\cos \theta\hspace{27pt} (3b)\)
\( \small \tan \left(\theta+180^{\circ}\right)=\tan \theta\hspace{34pt} (3c)\)

\( \small \sin \left(\theta-180^{\circ}\right)\) \(\small=-\sin \theta\hspace{29pt} (3d)\)
\( \small \cos \left(\small \theta-180^{\circ}\right)\) \(=\small -\cos\theta\hspace{27pt} (3e)\)
\( \small \tan \left(\theta-180^{\circ}\right)\) \(\small=\tan \theta\hspace{34pt} (3f)\)

\( \small (3g)(3h)(3i)\)は \( \small (3a)(3b)(3c)\) と同じです。
\( \small \sin \left(180^{\circ}+\theta\right)=-\sin \theta\hspace{29pt} (3g)\)
\( \small \cos \left(180^{\circ}+\theta\right)=-\cos \theta\hspace{27pt} (3h)\)
\( \small \tan \left(180^{\circ}+\theta\right)=\tan \theta\hspace{34pt} (3i)\)

\( \small (3j)(3k)(3l)\)は\(\small(3d)(3e)(3f)\) に対して角度の正負が反対なので、 \( \small (3d)(3e)(3f)\)に対して \(\small\cos\)は符号が変わらず、\(\small\sin\)と\( \small \tan\)は符号が変わる。※ \(\small\cos\) だけ符号が変わらないのは\( \small (1a)(1b)(1c)\) を参照。
\( \small \sin \left(180^{\circ}-\theta\right)\) \( \small =\sin \theta\hspace{38pt} (3j)\)
\( \small \cos \left(180^{\circ}-\theta\right)\) \( \small =-\cos \theta\hspace{28pt} (3k)\)
\( \small \tan \left(180^{\circ}-\theta\right)\) \( \small =-\tan \theta\hspace{26pt} (3l)\)

（参考） sin(180°-θ) = sin(-(θ-180°)) ＝-sin(θ-180°) = sin(θ)

なお、\( \small (3j)(3k)(3l)\)は、後述の「おまけA」も参考にしてください。

(4) \(\small\theta±90^{\circ} ,\hspace{8pt} 90^{\circ}±\theta\)

\( \small \sin \left(\theta+90^{\circ}\right)= \sin \left(\theta-(-90^{\circ}\right)) \) なので、 \( \small \sin \left(\theta+90^{\circ}\right)\) は、\( \small \sin \left(\theta\right) \)を\(\small -90^{\circ} \)平行移動したグラフです。つまり、 \(\small\sin\) よりも位相が \(\small 90^{\circ} \) 遅れた \(\small\cos\)と重なり、符号は変わりません。

一方、\( \small \cos \left(\theta+90^{\circ}\right)= \cos \left(\theta-(-90^{\circ}\right)) \) なので、 \( \small \cos \left(\theta+90^{\circ}\right)\) は\( \small \cos \left(\theta\right) \)を \(\small -90^{\circ} \) 平行移動したグラフです。つまり、 \(\small\sin\) との位相の差は \(\small 180^{\circ} \) に広がり、符号が変わります。

なお、 \( \small \tan(\theta) \) と \(\small \dfrac{1}{\tan \theta} \)は、グラフを見ても分かるように符号が同じです。しかし、 \( \small \tan \left(\theta+90^{\circ}\right) \)は \( \small \tan(\theta) \) の位相を\(\small 90^{\circ} \)ずらすため、 \( \small \tan \left(\theta+90^{\circ}\right) \) と \(\small \dfrac{1}{\tan \theta} \) の符号が反対になります。

\( \small \sin \left(\theta+90^{\circ}\right)\) \(\small=\cos \theta \hspace{39pt}\) \(\small(4a) \)
\( \small \cos \left(\theta+90^{\circ}\right)=-\sin \theta \hspace{33pt} (4b) \)
\( \small \tan \left(\theta+90^{\circ}\right)=-\dfrac{1}{\tan \theta} \hspace{30pt} (4c) \)

同様に\( \small \sin \left(\theta-90^{\circ}\right) \) は、 \( \small \sin \left(\theta\right) \)を\(\small 90^{\circ} \)平行移動したグラフです。つまり、 \(\small\cos\)との位相の差は\(\small 180^{\circ} \)に広がり、符号が変化します。

一方、 \( \small \cos \left(\theta-90^{\circ}\right)\) は、\( \small \cos \left(\theta\right) \)を \(\small 90^{\circ} \) 平行移動したグラフであり、 \(\small\sin\) と重なるため符号は変わりません。

なお、\(\small(4f) \)式は \( \small \tan \) の位相が \(\small 90^{\circ} \)ずれ、符号が変化します。

\( \small \sin \left(\theta-90^{\circ}\right)\) \( \small =-\cos \theta \hspace{35pt} (4d) \)
\( \small \cos \left(\theta-90^{\circ}\right)\) \( \small =\sin \theta \hspace{42pt}\) \(\small(4e) \)
\( \small \tan \left(\theta-90^{\circ}\right)\) \( \small =-\dfrac{1}{\tan \theta} \hspace{31pt} (4f) \)

\(\small (4g)(4h)(4i)\) は\(\small (4a)(4b)(4c)\) と同じ

\( \small \sin \left(90^{\circ}+\theta\right)=\cos \theta \hspace{43pt} (4g) \)
\( \small \cos \left(90^{\circ}+\theta\right)=-\sin \theta \hspace{34pt} (4h) \)
\( \small \tan \left(90^{\circ}+\theta\right)=-\dfrac{1}{\tan \theta} \hspace{31pt} (4i) \)

\( \small (4j)(4k)(4l)\)は\(\small(4d)(4e)(4f)\) に対して角度の正負が反対なので、 \( \small (4d)(4e)(4f)\)に対して \(\small\cos\)は符号が変わらず、\(\small\sin\)と\( \small \tan\)は符号が変わる。※ \(\small\cos\) だけ符号が変わらないのは\( \small (1a)(1b)(1c)\) を参照。
なお、\(\small \left(90^{\circ}-\theta\right)\) は、結果が全てプラスになると覚えてもよいと思います。

\(\small\sin \left(90^{\circ}-\theta\right)\) \( \small =\cos \theta \hspace{44pt} (4j) \)
\(\small\cos \left(90^{\circ}-\theta\right)\) \( \small =\sin \theta \hspace{44pt} (4k) \)
\(\small\tan \left(90^{\circ}-\theta\right)\) \( \small =\dfrac{1}{\tan \theta} \hspace{39pt} (4l) \)

（参考） sin(90°-θ) = sin(-(θ-90°))=-sin(θ-90°)=cos(θ)

なお、\( \small (3j)(3k)(3l)\)は、後述の「おまけB」も参考にしてください。

(5) sin(-90°-θ), sin(-θ-180°)などは？

sin(-90°-θ)やsin(-θ-180°)などは、今まで出てきませんでしたが、どのように計算すればよいのでしょうか。

これらの式は、今までの公式を使って以下のように計算することができます。

sin(-90°-θ) = sin(-(90°+θ)) = -sin(90°+θ) = cos(θ)

sin(-θ-180°) = sin(-(θ+180°))=-sin(θ+180°)=sin(θ)

2. まとめ

ここまでの内容を理解できたら、この「まとめ」の部分だけを繰り返し読んで覚えましょう。

(1) cosはy軸に対して線対称なので符号は変わらない。
\(\small \sin (-\theta)=-\sin \theta\hspace{50pt} (1a)\)
\(\small \cos (-\theta)=\cos\theta\hspace{57pt}(1b)\)
\(\small \tan (-\theta)=-\tan \theta\hspace{46pt}(1c)\)

(2) sin,cosの周期は360°、tanの周期は180°なので符号は変わらない。
\( \small \sin \left(\theta±360^{\circ}\right)=\sin \theta \hspace{37pt} (2a)(2d) \)
\( \small \cos \left(\theta±360^{\circ}\right)=\cos \theta \hspace{35pt} (2b)(2e) \)
\( \small \tan \left(\theta±360^{\circ}\right)=\tan \theta \hspace{33pt} (2c)(2f) \)

(3) 180°はsin,cosは周期360°の半分なので、sin, cosだけ符号が変わる。
\( \small \sin \left(\theta±180^{\circ}\right)=-\sin \theta\hspace{29pt} (3a)(3d)\)
\( \small \cos \left(\theta±180^{\circ}\right)=-\cos \theta\hspace{27pt} (3b)(3e)\)
\( \small \tan \left(\theta±180^{\circ}\right)=\tan \theta\hspace{34pt} (3c)(3f)\)

(4) \( \small \sin \left(\theta+90^{\circ}\right)\) は、\( \small \sin \left(\theta\right) \)を\(\small -90^{\circ} \)平行移動したグラフであり、\( \small \cos \left(\theta-90^{\circ}\right)\) は、\( \small \cos \left(\theta\right) \)を\(\small 90^{\circ} \)平行移動したグラフなので、符号は変わらない。
\( \small \sin \left(\theta+90^{\circ}\right)\) \(\small=\cos \theta \hspace{39pt}\) \(\small(4a) \)
\( \small \cos \left(\theta+90^{\circ}\right)=-\sin \theta \hspace{33pt} (4b) \)
\( \small \tan \left(\theta+90^{\circ}\right)=-\dfrac{1}{\tan \theta} \hspace{30pt} (4c) \)
\( \small \sin \left(\theta-90^{\circ}\right)\) \( \small =-\cos \theta \hspace{35pt} (4d) \)
\( \small \cos \left(\theta-90^{\circ}\right)\) \( \small =\sin \theta \hspace{42pt}\) \(\small(4e) \)
\( \small \tan \left(\theta-90^{\circ}\right)\) \( \small =-\dfrac{1}{\tan \theta} \hspace{31pt} (4f) \)

θが後ろにくる場合など、他のタイプは計算で簡単に求められるので覚える必要はありません。

以下、おまけA, B, Cは覚える必要はありませんが、理解を深めるために目を通してください。おまけCは語呂合わせによる暗記法です。

3. おまけA: 180°-θの符号をグラフから読み解く

180°-θの符号もグラフで確認してみましょう。

\( \small \sin \left(180^{\circ}-\theta\right)\) \( \small =\sin \theta\hspace{38pt} (3j)\)
\( \small \cos \left(180^{\circ}-\theta\right)\) \( \small =-\cos \theta\hspace{28pt} (3k)\)
\( \small \tan \left(180^{\circ}-\theta\right)\) \( \small =-\tan \theta\hspace{26pt} (3l)\)

下図は「x=180°-θ」と「x=θ」のグラフです。この図を見れば、sinは符号が変わらず、cos, tanは符号が変わることが明白です。

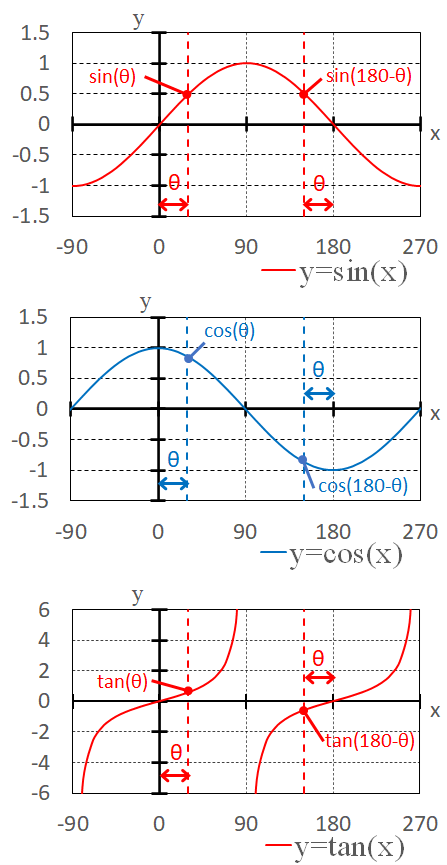
なお、y=sin(x)は、x=90°の直線に関して線対称となっており、y=cos(x), y=tan(x)は(x, y) = (90°, 0)に関して点対称となっています。

4. おまけB: 90°-θの符号をグラフから読み解く

90°-θのグラフを見てみましょう。y=sin(x)とy=cox(x)は、x=45°の直線に関して線対称となっており、同様にy=tan(x), y=1/tan(x)もx=45°の直線に関して線対称となっています。

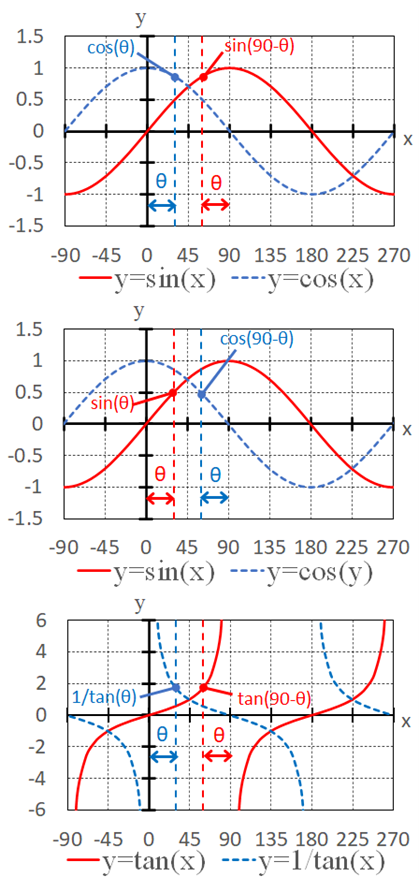
ただし、90°-θについてはグラフからは少しイメージをつかみにくいので、sin(90°-θ)、cos(90°-θ) 、tan(90°-θ)の結果はすべてプラスになると覚えた方がよいかもしれません。

5. おまけC: θ±90°、90°±θの語呂合わせ

おまけです。語呂合わせを考えてみました。\(\small\theta±90^{\circ} ,\hspace{8pt} 90^{\circ}±\theta\) の公式では、符号が変わらないものを以下のように覚えることもできます。ただ、語呂合わせだけに頼らないようにしましょう。

「ナンシー」は「サンタ」が「こない」けどプラス思考。

\( \small \sin \left(90^{\circ}+\theta\right)\) \(\small=\cos \theta \hspace{43pt} (4g) \)
\( \small \cos \left(90^{\circ}+\theta\right)=-\sin \theta \hspace{34pt} (4h) \)
\( \small \tan \left(90^{\circ}+\theta\right)=-\dfrac{1}{\tan \theta} \hspace{31pt} (4i) \)

\(\small\sin (90^{\circ}\) \(\small-\theta)\) \( \small =\cos \theta \hspace{44pt} (4j) \)
\(\small\cos (90^{\circ} \) \(\small -\theta)\) \( \small =\sin \theta \hspace{44pt} (4k) \)
\(\small\tan (90^{\circ} \) \(\small -\theta)\) \( \small =\dfrac{1}{\tan \theta} \hspace{39pt} (4l) \)