Python♪基本：大切なものは「宝箱」に保管するテクニック

プログラミングは、文法が全てではありません。基本的なテクニックを身につけることも大切です。最大値や最小値を求めるような問題では、必要なデータをif分で抽出し「宝箱」に保管しておくテクニックがあります。単純で、かつ、強力な方法ですので、例題を見ながらこの基本テクニックを自分のものにしてしまいましょう。

色々な場面で使うことができる基本的なテクニックですので、このテクニックを自由自在に扱えるようになってください。今回は演習を中心に進めたいと思います。

私「ゆうちゃん。- x ** 2 + 4 * x - 1 のxの値が自由にかわるとして、最大値がいくらになるかわかる？」
ゆうちゃん「そんなの、わからないよ。習ってないし～。（即答）」
私「習ってないのは知ってる。これは高校で勉強するんだけど、でも、ちょっとは、考えてみてよ～。ゆうちゃんなら大丈夫。」

（おだてて、考えさせるつもりだったんだけど失敗。ゆうちゃんは、やる気喪失。とりあえず、お茶とお菓子の時間にしました。どうやら任天堂switchが欲しいのに、買ってもらえなくて、やる気が出ないとのこと。）

ゆうちゃん「・・・・・・。でも、どうしても考えろと言われたら、いろいろ、試してみるぐらいしか思いつかないけど・・・」

私（おっ、やった！）「そう！そのとおりなのよ。」（相変わらず、勘がするどいわね・・・）
ゆうちゃん「えっ！」（目がきらりん）
私「数学だと、式を変形したり、微分というテクニックを使ったり大変（?）なんだけど、Python使うときは、ひたすら計算して、その中で一番大きい答えを最大値って、思えばいいのよ。」
ゆうちゃん「ふーん・・・」（斜め右上を見上げて考えている）
私「人間だと、100回計算しろっていうと、やる気なくすけど、コンピューターって、同じことをやるのが得意だから。やらせちゃえばいいのよ。」
ゆうちゃん「そんなもんなのかな・・・。少し、かわいそうな気もする。」
私「コンピューターで計算すると、バシッと正解がでるイメージがあるけど、だいたい、合ってればO.K.っていうのが、コンピューターなのよね。」
ゆうちゃん「だいたいしか分からないんじゃ、学校のテストは零点だね。」
私「いいのよ、いいのよ、世の中なんて、だいたい分かればO.K.なの。」
ゆうちゃん「へぇ～。世の中って、適当なんだ。」
私「ちょっと、変に伝わったかもしれないけど、そうなのよ。」
ゆうちゃん「うそうそ、わかってるよ。」

（今日のゆうちゃんは、ちょっとテンション低めだけど、復活してきました。）

０．ゆうちゃんとPythonシリーズ

この記事は「ゆうちゃんとPythonシリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。

中学生のゆうちゃんとPythonシリーズ

なお、それぞれの記事は、シリーズの中でそれまでに習った文法を使ってサンプルコードを考えています。実際には、もっと、効率のよい書き方があるかもしれませんが、ご了承ください。

1．例題の設定

あるところに研究熱心な愛のキューピットがおりました。射程距離が短い弓矢では、なかなか、愛の矢が当たらないので、愛の大砲を発明しました。この大砲は空気抵抗などは受けない愛の砲弾を撃つことができ、その威力は絶大です。

大砲は火薬の量で、砲弾の最初の速度を変えることはできますが、発射角は45度固定です。以下の図のように、城壁の上からターゲットに向けて発射されます。

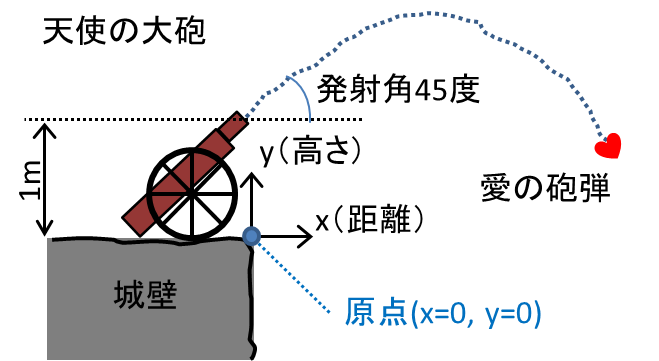
この場合の弾道は、原点(x=0, y=0)を城壁の角の部分とすると、水平距離xと高さyの関係を以下の式であらわすことができます。大砲の筒先までの高さが1mなので、式の最後が「+1」になっています。

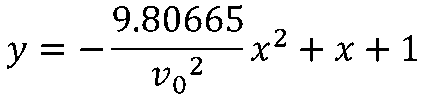
x, yの単位は(m)、砲弾が大砲を飛び出すときの初速（v₀）の単位は（m/秒）です。

「ゆうちゃん、ちなみに、本当にこんな式になるんだよ～」

2．例題1（弾道のグラフ化）

初速v0が毎秒25mのとき、砲弾がどのように飛ぶか、x(水平距離)とy(高さ)の関係をグラフにしましょう。なお、0≦x≦70 の範囲とします。つまり、筒先を飛び出して70m先までの砲弾の弾道をグラフ化することになります。
また、v0(=25)が決まれば、残る変数はxとyだけになるので、xとyの関係がわかりますね。それをグラフにするということです。

なお、基本：簡単なfor文とrandom関数を使ってグラフを表示しよう で紹介した以下コード11を参考にしてください。

#コード11
import random
import matplotlib

for i in range(1000):
    x = random.uniform(-1.0, 1.0)
    y = x ** 2
    matplotlib.pyplot.plot(x, y, marker='.')
matplotlib.pyplot.show()

当然、コード11は、大砲の弾道を示す式ではないので、改良が 必要ですが、でも、少しだけ変えれば良いだけなので考えてみてください。

(1) 例題1の解答例

以下、解答例です。「解答の表示・非表示の切り替え」の部分をクリックすると、解答例が表示されます。

解答の表示・非表示の切り替え (Google Chrome推奨)

==============(解答表示start)==============

いかがでしょうか。6, 7行目が変わっただけですね。

#コード01
import random
import matplotlib

for i in range(1000):
    x = random.uniform(0.0, 70.0)
    y = - 9.80665 / 25.0 ** 2 * x ** 2 + x + 1
    matplotlib.pyplot.plot(x, y, marker='.')
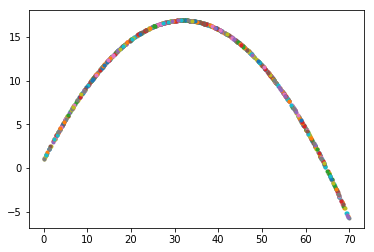
matplotlib.pyplot.show()

以下、出力結果です。高さの最大値は約15m、また、高さがマイナスにならない範囲の飛距離は60mぐらいありそうです。

出力01

==============(解答表示end)===============
※ブラウザによっては、最初から解答が表示されてしまう可能性があります。

(2) コード01の書式を整える

コード01は、短いコードなので問題ないのですが、もっと長いコードならば、こんな書き方はしません。長いコードは、例え自分で書いたコードでも、忘れてしまいます。その度にコードの内容を読み直していたら、時間がいくらあっても足りません。大切なのは「何をするプログラムなのか」がわかること。そして、「入力」「出力」が明快なことです。これらが明快であれば、計算の中身がわからなくても、再利用可能な使いやすいコードになります。

以下、コード01を私なりに書き換えてみました。コードの新旧を判別するために、コードを作成した日付も入れてあります。

コードの行数は長くなりますが、コード02のような書き方をすれば21～24行目の計算内容が分からなくても、このプログラムを使うことができます。計算の部分が長く、複雑になればなるほど、入力部と出力部を明快に分けることで、再利用しやすいプログラムにすることができます。

また、変数名を意味の分かるx_min, x_max, v0とすることで、22, 23行目の命令文がなにをしている行なのかを想像しやすくなります。

更に23行目の計算式にはカッコをつけました。この例ではカッコがなくても同じ結果になりますが、私は、カッコがあった方が見やすい場合には、積極的にカッコをつけるようにしています。計算式の記述ミスは致命的なので、見やすさを優先しています。

#コード02
'''天使の大砲の軌道グラフ化プログラム

発射角が45度の場合の弾道をグラフ化(2019.6.9)
(1)入力
 x_min:水平距離の最小値(m)
 x_max:水平距離の最大値(m)
 v0:砲弾の初速(m/秒)
 n_cal_i:繰り返し計算回数。（水平距離をランダムに与える）(回)
(2)出力
 砲弾の軌道のグラフ
'''
import random
import matplotlib

#入力
x_min = 0.0
x_max = 70.0
v0 = 25.0
n_cal_i = 1000

#計算
for i in range(n_cal_i):
    x = random.uniform(x_min, x_max)
    y = - 9.80665 / (v0 ** 2) * (x ** 2) + x + 1
    matplotlib.pyplot.plot(x, y, marker='.')

#描画、出力
matplotlib.pyplot.show()

コード02の2～12行目ではプログラムの説明を行っていますが、コードの最初に記述することで、実はこの説明文を別のコード（モジュール）から呼び出すことができます。なお、この説明文はドキュメンテーション文字列と呼ばれ、推奨される書き方があります。 せっかくなら、最初から推奨される書き方で記述したほうがよいのではないでしょうか。

ドキュメンテーション文字列 の書き方を簡単に説明すると、 まず、コード02の2行目のように、最初の「'''」と同じ行に簡潔な説明を加えます。そして、次の行は空白行にします。最後に、空白行のあとに、必要な説明を自由に記述します。なお、最後の「'''」 は 12行目のように 単独で記述します。

一方、プログラムの説明を1行だけで終わらせる場合は、以下の例のように、 説明文を「'''」ではさみ、全てを1行で完結させます。

'''天使の大砲の軌道グラフ化プログラム'''

入力する数値の単位がわからなかったり、説明のないプログラムは後で読み返すのが大変です。一手間かかりますが、プログラムの説明を記述する習慣をつけましょう。

3．例題2（砲弾の高さの最大値）

いよいよ、大切なものを「宝箱」に保管する例題です。求めるのは砲弾の高さの最大値です。

最大値を求める方法は、以下の通りです。
コード02では、1000回もくりかえし計算をしています。そして、コード02の出力02は、1000回の計算結果をプロットしたものですが、図にプロットされた1000回の計算のうち、一番高さ(y)が大きいものを最大値であると考えます。出力02のグラフを見てもわかるように、最大高さを精度良く求めることができそうです。なお、計算回数が多いほど、答の精度があがります。

出力02

もっと、具体的に説明すると、まず、y_maxという変数（宝箱）を用意します。そして、くりかえし計算の中で、数値が大きいyが見つかるたびに、宝箱(y_max)の数値を更新します。すると、計算が終わったあとに宝箱(y_max)に残っている数値が最大値ということになります。なお、宝箱の更新の判定はif文を使います。

高さ最大値の理論値は、y_max = 16.933065827780133です。この値に近い値が答として求められれば正解です。

(1) ヒント

もし、「NameError: name 'y_max' is not defined」というエラーが発生して、解決法がわからない場合には、以下のヒントを見てください。

(2) 解答例

解答例は以下の通りです。分からなかった人は解答を見るだけではなく、実際に入力して実行してみましょう。

#コード03
'''天使の大砲の軌道グラフ化、最高高さ算出

発射角が45度の場合の弾道グラフ化、最高高さ算出(2019.6.9)
(1)入力
 x_min:水平距離の最小値(m)
 x_max:水平距離の最大値(m)
 v0:砲弾の初速(m/秒)
 n_cal_i:繰り返し計算回数。（水平距離をランダムに与える）(回)
(2)出力
 砲弾の軌道のグラフ
 y_max:最高高さ(m)
'''
import random
import matplotlib

#入力
x_min = 0.0
x_max = 70.0
v0 = 25.0
n_cal_i = 1000

#計算
x = random.uniform(x_min, x_max)
y_max = - 9.80665 / (v0 ** 2) * (x ** 2) + x + 1
for i in range(n_cal_i):
    x = random.uniform(x_min, x_max)
    y = - 9.80665 / (v0 ** 2) * (x ** 2) + x + 1
    matplotlib.pyplot.plot(x, y, marker='.')
    if y_max < y:
        y_max = y

#描画、出力
matplotlib.pyplot.show()
print('yの最大値：',y_max)

(3) 解答精度

以下、理論値と、コード03による解の10回分を並べたものです。なお、単位はm（メートル）です。それぞれ、1000回分のランダム計算の結果なので、毎回、計算結果は異なります。しかし、10回分の結果からみると、理論値と比較して誤差は1mm以下です。

 　理論値： 16.93306573949838
yの最大値： 16.933028945540503
yの最大値： 16.933007654132048
yの最大値： 16.932821347075357
yの最大値： 16.9329699809509
yの最大値： 16.933052723343835
yの最大値： 16.933043431749013
yの最大値： 16.93290520222155
yの最大値： 16.933050839733397
yの最大値： 16.933065508503034
yの最大値： 16.93299612007766

なお、コード03は計算時間が少し長いかもしれません。これは、グラフの描画に関係する部分が遅いためです。 グラフは表示されなくなりますが、 15, 29 ,34行目を「#」でコメントアウトすると、計算速度は格段に速くなります。計算速度を上げたい場合には試してみてください。

4．例題3（砲弾の高さが最大値の時の水平距離）

例題2では、砲弾の高さの最大値を求めましたが、そのときの水平距離も求めましょう。具体的には高さyの最大値だけではなく、そのときの水平距離xも求めるプログラムです。コード03を改良し、x_ymaxという宝箱をもう一つ用意すれば完成です。

なお、水平距離xの計算では、高さのときよりも誤差が大きいので、繰り返し計算回数は10000回としましょう。また、10000回では計算時間が長いため、グラフ描画に関係する行は「#」によりコメントアウトしましょう。

(1) 解答例

理論値は、砲弾の高さの最大値 = 16.933065827780133、その時の水平距離 = 31.86613165556026 となります。この値に近い値になれば正解です。

#コード04
'''天使の大砲の軌道グラフ化、最高高さ位置の座標算出

発射角が45度の場合の弾道をグラフ化、最高高さ位置の座標算出(2019.6.9)
(1)入力
 x_min:水平距離の最小値(m)
 x_max:水平距離の最大値(m)
 v0:砲弾の初速(m/秒)
 n_cal_i:繰り返し計算回数。（水平距離をランダムに与える）(回)
(2)出力
 砲弾の軌道のグラフ
 y_max:最高高さ(m)
 x_max:最高高さでの水平距離(m)
'''
import random
#import matplotlib

#入力
x_min = 0.0
x_max = 70.0
v0 = 25.0
n_cal_i = 10000

#計算
x = random.uniform(x_min, x_max)
x_ymax = x
y_max = - 9.80665 / (v0 ** 2) * (x ** 2) + x + 1
for i in range(n_cal_i):
    x = random.uniform(x_min, x_max)
    y = - 9.80665 / (v0 ** 2) * (x ** 2) + x + 1
#    matplotlib.pyplot.plot(x, y, marker='.')
    if y_max < y:
        x_ymax = x
        y_max = y

#描画、出力
#matplotlib.pyplot.show()
print('yの最大値：',y_max)
print('水平距離x：',x_ymax)

(2) 解答精度

以下、10回分の計算結果です。砲弾が最大高さになるときの水平距離を抜き出しています。それぞれ、10000回計算すると、誤差が10mm以下ぐらいにはなっているようです。

　理論値x： 31.86613165556026
水平距離x： 31.868601642370923
水平距離x： 31.861739115265358
水平距離x： 31.86562062670291
水平距離x： 31.869346823001678
水平距離x： 31.865335656428638
水平距離x： 31.87324365279664
水平距離x： 31.86775062223724
水平距離x： 31.865417504106897
水平距離x： 31.86237414764944
水平距離x： 31.86734642459102

５．例題４（城壁の高さに対する砲弾の飛距離）

例題4では、砲弾の初速が25m、城壁が5mのときの飛距離を求めてください。 今までと同じようなやりかたで答を出すことができるので考えてみましょう。

また、地面はどこまでも平らで、傾斜はないものとします。つまり、5mの城壁から見ると、地面は5m下にあることになります。なお、繰り返し計算回数は10000回とし、グラフ化はしません。

(1) ヒント

慣れていないと、すぐには思い浮かばないかもしれません。この問題は、 いかに 大切なデータを宝箱に保管するかがポイントです。どうしても、わからない場合は、ヒントを開いてみましょう。

(2) 解答例

以下、解答です。飛距離の理論値は69.25388268mになります。
なお、理論値は中３で習う解の公式を使い、- 9.80665 / (25 * 25) * x ** 2 + x + 1 = - 5を解けば出ますが、公式なんか知らなくても、Pythonで解けちゃうんです。

#コード05
'''天使の大砲の飛距離算定プログラム

発射角が45度、城壁の高さがわかる時の飛距離計算プログラム(2019.6.9)
(1)入力
 x_min:水平距離の最小値(m)
 x_max:水平距離の最大値(m)
 v0:砲弾の初速(m/秒)
 h_wall:城壁の高さ(m)
 n_cal_i:繰り返し計算回数。（水平距離をランダムに与える）(回)
(2)出力
 x_hikyori:飛距離(m)
'''
import random

#入力
x_min = 0.0
x_max = 70.0
v0 = 25.0
h_wall = 5.0
n_cal_i = 10000

#計算
x_hikyori = x_min
for i in range(n_cal_i):
    x = random.uniform(x_min, x_max)
    y = - 9.80665 / (v0 ** 2) * (x ** 2) + x + 1
    if (x_hikyori < x) and (- h_wall < y):
        x_hikyori = x

#出力
print('飛距離：', x_hikyori)

(3) 解答精度

以下、10回分の計算結果です。問題の無い（?）誤差なのではないでしょうか。もっと、精度をあげたいときには、計算回数を増やしましょう。

理論値： 69.25271553471711
飛距離： 69.24505197966747
飛距離： 69.24756527700453
飛距離： 69.2343898109208
飛距離： 69.25022436181669
飛距離： 69.24896351654006
飛距離： 69.25145618030376
飛距離： 69.25337413861021
飛距離： 69.25184620941472
飛距離： 69.24890718526349
飛距離： 69.24354197258512

ゆうちゃんは、最後の例題で少し苦戦していました。考え方は合っているのに、X座標とY座標を逆に考えてしまい、そのミスを見つけきれず、私がヒントをあげました。考え方がわからないというよりは、バグ消しに慣れていないのだと思います。

でも、他の例題は、なんとか自力で出来ていたので、すごいなあと思います。

なお、見やすい書式を書くために説明した、ドキュメンテーション文字列には興味がないご様子。

わたし「ゆうちゃん、今日のところわかった？」
ゆうちゃん「完璧！」
わたし「じゃあ、ドキュメンテーション文字列ってなに？書き方わかる？」
ゆうちゃん「えっと・・・、わかってるよ。」（ちょっと、目がおよぐ）
わたし「わかってないでしょ～。」
ゆうちゃん「ばれた～？」（サンプルコードを、探し始める）
わたし「次、また、聞くわよ～。」
ゆうちゃん「はい、は～い。まかせといて。」

ゆうちゃん、地味だけど、大事だから覚えといてね。

６．まとめ

いかがでしょうか。for文で何度も計算させ、if文によって必要なデータを宝箱に保管するテクニックは、様々なところで活用できます。ポイントとしては、１つめのデータだけは、 最初に for文の外で入れる必要があることです。
頭で理解するのではなく、例題をよく読んで、自分で実際にコードを記述してみることが大切です。

「2．例題1（弾道のグラフ化）」の「(2) コード01の書式を整える」では、 ドキュメンテーション文字列の書き方や、コードの入力部や出力部を明快に分ける書き方を説明しました。後で読み返しやすいコードにするのは重要なことです。

ホームページでサンプルプログラムを掲載するときは、シンプルさを優先し、この記事のような書き方ができないことも多いのですが、コードの最初にドキュメンテーション文字列 を記述し、プログラムの概要を説明する習慣をつけましょう。

ドキュメンテーション文字列 の書き方を簡単に説明すると、 まず、最初の「'''」と同じ行に簡潔な説明を加えます。そして、次の行は空白行にします。最後に、空白行のあとに、必要な説明を自由に記述します。なお、最後の「'''」 は 単独で記述します。

'''天使の大砲の軌道グラフ化プログラム

発射角が45度の場合の弾道をグラフ化(2019.6.9)
(1)入力
 x_min:水平距離の最小値(m)
 x_max:水平距離の最大値(m)
 v0:砲弾の初速(m/秒)
 n_cal_i:繰り返し計算回数。（水平距離をランダムに与える）(回)
(2)出力
 砲弾の軌道のグラフ
'''

説明が1行で終わる場合は、 以下の例のように、 説明文を「'''」ではさみ、全てを1行で完結させます。

'''天使の大砲の軌道グラフ化プログラム'''

私が実際に購入した教材のご紹介

以下、私が実際に購入したPythonの教材をまとめてみました。 Pythonを学習する上で、少しでもお役に立つことができればうれしいです。

・Python♪私が購入したPythonの書籍のレビュー
・UdemyのPythonの動画講座を書籍を買う感覚で購入してみた

その他

・Twitterへのリンクです。SNSもはじめました♪

液晶ペンタブレットを買いました
　(1) モバイルディスプレイを買うつもりだったのに激安ペンタブレット購入

以下、私が光回線を導入した時の記事一覧です。
　(1) 2020年「光回線は値段で選ぶ」では後悔する ←宅内工事の状況も説明しています。
　(2) NURO光の開通までWiFiルーターを格安レンタルできる
　(3) NURO光の屋外工事の状況をご紹介。その日に開通！
　(4) 光回線開通！実測するとNURO光はやっぱり速かった
　(5) ネット上のNURO光紹介特典は個人情報がもれないの？