Python♪FEM:微小変形の仮定と人の感覚の違い

有限要素法のプログラムの自作にチャレンジするなら、「微小変形」は必ず理解しましょう。人間の感覚と合わないので内容を知らなければ苦労します。解析では常識に近い初歩的なことなので書籍やサイトなどでも説明が省略されていることが多いです。

この記事では、「微小変形？なにそれ？」という方への導入として、微小変形の仮定と人の感覚の違いについて説明したいと思います。

０． FEMなど数値解析シリーズ
１．微小変形の仮定のもとでは変形が無限大？
２．現実の世界の剛性
２．微小変形の仮定における剛性
３．有限要素法における微小変形の仮定
私が実際に購入した教材のご紹介
その他

０． FEMなど数値解析シリーズ

この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。

Python♪FEMなど数値解析シリーズ

１．微小変形の仮定のもとでは変形が無限大？

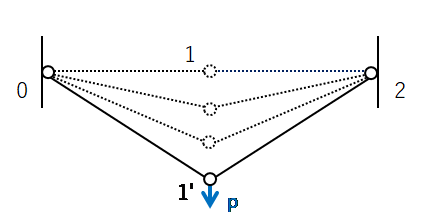
例題1（下図）のように、両端(節点0, 2)と中央(節点1)がピン接合されているトラスがあったとします。このトラスの節点1の部分に鉛直下向きの荷重を加えるとどうなるのでしょうか。

[例題1]

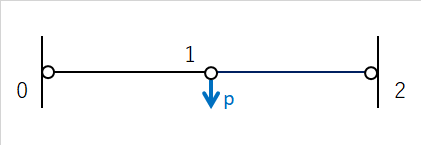
答は現実の世界では荷重pに対して節点1が節点1'の位置に移動して釣り合います。しかし、微小変形の仮定のもとでは、荷重pに対する節点１の変位は無限大になります。

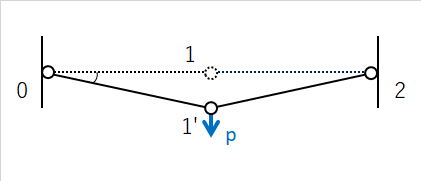
２．現実の世界の剛性

それでは、まず、上記の例題について現実の世界ではどのようになるか考えてみます。

載荷前のトラス部材は完全に水平です。トラス部材の両側はピンであり、部材には軸力しか生じませんので、節点1の変位がないときには外力に抵抗できる部材の鉛直応力成分はなく、荷重pに対する剛性はゼロです。

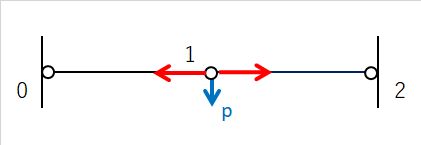
節点1の変位により部材に傾きθが生じると、今度は部材の軸力は鉛直成分と水平成分にわけることができるため、荷重pに対しても抵抗できるようになります。下の図ではトラス部材の軸力Nに対して、鉛直成分は2N・sinθであり、剛性も部材剛性kに対して 2k・sinθ です。つまり、荷重pに対する剛性はθに依存し、θが大きくなるほど剛性が高くなるのです。したがって、荷重と節点変位の関係は線形（比例）ではなく非線形の関係になります。

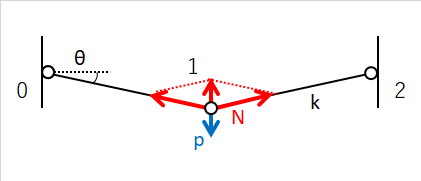
このような非線形性を幾何学的非線形といい、材料の塑性化などを要因とする材料非線形とは分けて考えます。

２．微小変形の仮定における剛性

ここまでの説明のとおり、物体に荷重をかけたとき、本来は物体の変形により剛性が絶えず変化します。しかし、その変化を考慮して構造物の解析を行うのは大変です。計算時間も増え、計算が発散してしまう可能性も高くなります。

そこで、「解析対象の変形による剛性の変化は考慮しない」という仮定が、微小変形の仮定です。つまり、解析対象の変形が無視できるほど小さいという仮定のもとに成り立っている考え方なのです。

それでは、微小変形の仮定は特殊な場合にしか使えないのかというとそうではありません。実はほとんどの計算は微小変形の仮定のもと行われています。例えば構造力学の梁の公式も剛性は一定です。つまり、これらも全て微小変形の仮定のもと成り立っている公式であり、微小変形の仮定を外れた解析を行うことのほうが特殊です。

さて、例題を振り返ってみましょう。すでに説明しましたが、節点1の変位がゼロの場合、外力に抵抗できる部材鉛直応力成分はなく、荷重pに対する剛性はゼロです。微小変形の仮定のもとでは、剛性は初期剛性のまま変化しませんので、どれだけ変形が進んでも荷重pに対する剛性はゼロのままなのです。つまり、変形は無限大となり不安定構造物です。

このような構造物は幾何学的非線形を考慮したプログラムで解析すれば答を出すことができます。しかし、力学的に無理がある構造は不経済な断面になるため実際の構造物で採用されることないでしょう。

３．有限要素法における微小変形の仮定

有限要素法では、基本的に外力から節点の変位を求め、節点の変位から部材の応力を求めます。そして、解を求めるためには力の釣り合いを考えなければなりませんが、微小変形の仮定を意識しながら考え方を整理する必要があります。

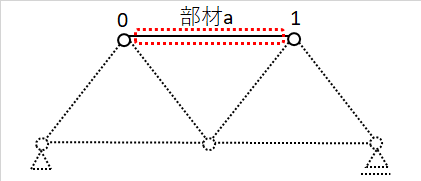
さて、それでは次に有限要素法のプログラムの中でどのようなモデル化が行われているかについて紹介したいと思います。今度は下図のようなトラスの部材aを切り出して、変形前と変形後の力の釣り合いを考えてみましょう。切断面は節点0, 節点1のすぐ内側です。

[例題2]

切り出した部材aの変形前と変形後の力の釣り合いは下図のとおりです。上図のトラス構造物に、なんらかの外力を加えた場合の部材aについて、載荷前と載荷後の荷重と変位の状況を図示しました。

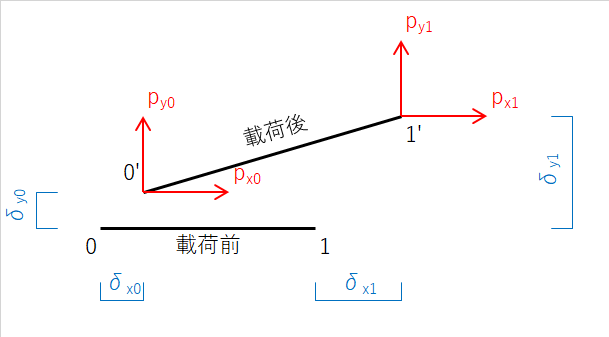
変形前は荷重も節点変位もゼロの状態です。一方、変形後は節点0はトラスの変形により節点0'に移動し、x方向の変位はδx0, y方向の変位はδy0です。同様に節点1は節点1'に移動し、x, y方向の変位はそれぞれδx1, δy1です。なお、切り出した部材の部材端0に生じる外力はx方向がpx0, y方向がpy0です。また、節点1側の部材端1に生じるx方向、y方向の外力はpx1, py1です。

このとき、微小変形の仮定のもと、「δx0, δy0, δx1, δy1」と「px0, py0, px1, py1」の関係を求めたいと思います。

まず、部材aのヤング係数をE、断面積をA、部材長をLとすると、部材の剛性kはE・A / L で求めることができますが、部材長さLは変形後ではなく変形前の部材長を用います。微小変形の仮定では剛性は変形前の形状から求めるため当然のことです。

k = E・A / L

次に、 px0, py0, px1, py1 から、部材の材軸方向に加わる外力と材軸に直交する方向の外力を求めたいと思いますが、部材の材軸方向とは部材の変形前と変形後のどちらの方向のことなのでしょうか。

荷重がかかった状態は変形後の状態なので、ついつい、変形後の部材の向きで考えてしまうかもしれませんがそれは誤りです。

微小変形の仮定では、変形前の形状から剛性を求め、荷重と変位の関係も全て変形前の形状で考えます。つまり、この例では変形前の部材が水平ですから、変形後の部材の傾きを考慮する必要はありません。部材端0と部材端1の材軸方向の外力は、それぞれpx0, px1であり、材軸に直交する方向の外力はそれぞれpy0, py1です。

同様に部材端0と部材端1の材軸方向の変位は、それぞれδx0, δx1であり、部材に直交する方向の変位はそれぞれδy0, δy1 です。上記の図をもう一度表示しますので、図を見ながら理解してください。

変形後の図で判断するとpx0やpx1が材軸方向の荷重には見えませんので注意しましょう。

では、力の釣り合い式を考えます。なお、上図ではpx0よりもpx1の方がわかりやすいため、px1を最初に求めます。水平右側が正だとすると、材軸方向の力の釣り合いは以下のようになります。

px1 =  k × (δx1 - δx0) 
    = k × (- δx0 + δx1)

px0はpx1と大きさが同じで向きが逆ですから下式となります。

px0 = - px1 = k × (δx0 - δx1)

では、材軸と直交方向の力の釣り合いはどのようになるのでしょうか。剛性は微小変形の仮定により載荷前の剛性を適用し、部材に直交する方向の剛性はゼロです。したがって、δy0, δy1の値にかかわらず、py0, py2はゼロとなります。もちろん、材軸方向の変位δx0, δx1は部材に直交する方向の力の釣り合いには影響は与えません。