平面トラスの有限要素法のプログラムをPythonで組んでみました。以前に自分がつくったコードを引っ張り出してきて、Pythonに移植しました。このくらいのボリュームのコードにじっくり取り組むと面白いです。
トラスのプログラムを実際に使うことは少ないかもしれませんが、最初のFEMコードはやはり平面トラスからです。平面トラスが組めれば、有限要素法の計算の流れがわかるので、立体フレームなどへの改良は簡単です。
0. FEMなど数値解析シリーズ
この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。
1.サンプルコードについて
以下、サンプルコードの書式について概要を説明したいと思います。
(1) コンセプト
このサンプルコードは、FEM解析の学習用です。FEMの基本的な考え方の習得が容易になる用に、以下のような方針でコードを作成しました。
- クラスは使用せずdef関数を用いる。
- データの入出力にファイルは使用しない。
- i, j, kのように、意味を持たないシンプルな変数名は使用しない。
なお、Pythonの数値解析では、解析速度を上げるためにfor文による深いネスト構造を避けます。Numpyを使えば、もう少しfor文を減らすことができるかもしれません。
(2) 可読性
Pythonの欠点として、変数のスコープが分かりにくいことが挙げられます。長いコードでは、関数への入力、関数からの出力をはっきり明示すべきです。
Pythonでは引数なしで外側の変数を内側から参照できます。ですから、このglobal変数を多用すれば関数の引数を激減させることも容易です。でも、データの流れがわかりにくくなります。
そこで、私は以下のような方針でコードを記述することにしました。
- global変数は不用意には使わない。
- 文法上不要であっても、関数に渡すデータは引数に記述する。例えばサンプルコードのdef set_gk(i_g_mn, siz_nod, ek_glo, mem_nn, gk)では、i_g_mn, siz_nod, ek_glo, mem_nn, gkはglobal変数なので引数は文法上不要ですが、関数の入力を明確にするために記述しました。
- 関数内で変更した変数はできるだけreturanで返す。Pythonでは2つ以上の変数でもreturanで返すことができるので、かなり柔軟に対応できます。
- 文法上不要であっても、関数から出力するデータはreturnで明示する。例えばgkはglobal変数なので、関数set_gk()において文法上は引数、returnへの記述は不要である。しかし、「gkを入力→gkの変更→gkの出力」の流れをはっきりさせるために、引数、returnで明示している。
ただし、入出力変数の数が多すぎる場合には関数内でglobal宣言を行うことで対応します。
- 関数への入力データが多すぎて、引数の記述が長すぎる場合には、引数の代わりに関数内でglobal宣言を行うことにより、入力する変数を明示します。→ 、def output_data()、def output_result()
- 関数からの出力データが多すぎる場合は、returnではなくglobal宣言を行うことにより、出力する変数を明示します。→ def input_data()、bc_index()
(3) その他の書式についての備考
- 1行の文字数は79文字以下(一般的な表記法と同じ)
- 一般的にはインデントは「半角スペース4文字」が推奨されていますが、数値解析では算定式が長くなる傾向にあり、文字数をかせぐために「半角スペース2文字」とする。
- あとで読み返すときに時間がかかるのが嫌いなのでコメント文は多めです。多分、多すぎると思います。本来は解説資料を別に作り、説明はシンプルにする方がプログラムの全体が見渡せてよいと思います。
- プログラムを使うにはファイルで入出力を行った方が楽です。でも、このトラスプログラムの用途はFEMの勉強ですので、小回りがきくようにデータを変数に直接代入しました。
- 少数(float)の出力書式で桁数の指定は行っていません。これはコードを試行錯誤する上で小数点以下の誤差がわかるようにしたかったからです。
- 最も解析に時間がかかるのは連立一次方程式の部分です。このサンプルコードではnumpy.linalg.solve()を使っています。NumPyは計算速度に定評のあるライブラリであり、たった1行で解が求まるのは本当に楽です。なお、規模の大きい構造物など解析時間が気になる場合には、反復法や、疎行列であることを利用した計算方法などを考えるとよいです。
- 入力データ例のdef datum()、def datum_exp01()において、ヤング係数eygは計算内容の検証で値がシンプルになるように1.0を入力しています。
サンプルコードの「if name == 'main':」以降の記述では、コードの流れがわかる目次のようになっていることが理想です。引数やreturnで明示することで全体的なデータの流れが分かりやすくなります。
一般的な記法ではないかもしれませんが、このような書き方でPythonの弱点を補うことをお勧めします。
2.サンプルコード
サンプルコードの紹介です。なお、変数名のアルファベットが何の略なのかについては、以下の記事を参考にしてください。サンプルコードで出てくる全ての変数を解説しました。力作です。
# -*- coding: utf-8 -*-
'''平面トラス解析プログラム Ver.1.04 (2021.2.11) by Snow Tree in June
平面トラスの節点変位、部材応力、反力の算定
'''
import numpy as np
def input_data_1():
'''入力データ例2(3節点、3部材トラスの例) ※適用範囲は32,767節点以下、65,535部材以下。
input_data: [INPUT][DATA]
(1) 入力データ
siz_nod(=2):節点自由度。x、y方向変位の2種類
var_max(=65535):部材数などで指定した変数の型が取り得る最大値
uint16→0~65535、unit36→0~4294967295、unit64→0~18446744073709551615
総節点数(nod_tn)は(var_max-1)/siz_nod以下、総部材数(nod_tn)は(var_max)以下。
nod_tn:総節点数
mem_tn:総部材数
bc_tn:境界条件を与える節点の数
nl_tn:外力が作用する節点の数
mem_ym :ヤング係数
nod_coo[i, j]:i節点の座標(j=0:x方向, j=1:y方向)
mem_are[i] :i部材の断面積
mem_nn[i, j]:i部材を構成する節点番号(j=0, 1)
bc_nn[i]:境界条件を与えられている節点番号
bc_ff[i, j]:fixの方向:0, freeの方向:1(j=0:x方向, J=1:y方向)
nl_nn[i]:外力が作用する節点番号
nl_mag[i, j]:外力の大きさ(j=0:x方向, J=1:y方向)
'''
#関数からの出力
global siz_nod, var_max
global nod_tn, mem_tn, bc_tn, nl_tn
global mem_ym
global nod_coo, mem_are, mem_nn, bc_nn, bc_ff, nl_nn, nl_mag
siz_nod = 2
var_max = 65535
nod_tn = 3
mem_tn = 3
bc_tn = 2
nl_tn = 1
mem_ym = 1.
#適用範囲の確認
if (nod_tn * siz_nod) > (var_max - 1):
print('error:節点数が適用範囲を超えている。nod_tn * siz_nod > var_max -1 ')
if mem_tn > var_max:
print('error:部材数が適用範囲を超えている。mem_tn > var_max')
#'uint16' 0~65535
#numpy配列の宣言
nod_coo = np.zeros((nod_tn, siz_nod), dtype = 'float64')
mem_are = np.zeros(mem_tn, dtype = 'float64')
mem_nn = np.zeros((mem_tn, 2), dtype = 'uint16')
bc_nn = np.zeros(bc_tn, dtype = 'uint16')
bc_ff = np.zeros((bc_tn, siz_nod), dtype = 'bool')
nl_nn = np.zeros(nl_tn, dtype = 'uint16')
nl_mag = np.zeros((nl_tn, siz_nod), dtype = 'float64')
nod_coo[:] = [[-100, 0],
[0, 100],
[100, 0]]
mem_are[:] = 100.
mem_nn[:] = [[0,1],
[1,2],
[0,2]]
bc_nn[:] = [2,0]
bc_ff[:] = [[1, 0],
[0, 0]]
nl_nn[0] = 1
nl_mag[0, :] = [0., -3.]
def input_data_2():
'''入力データ例2(5節点、7部材トラスの例) ※適用範囲は32,767節点以下、65,535部材以下。
適用範囲は32,767節点以下、65,535部材以下。
'''
#関数からの出力
global siz_nod, var_max
global nod_tn, mem_tn, bc_tn, nl_tn
global mem_ym
global nod_coo, mem_are, mem_nn, bc_nn, bc_ff, nl_nn, nl_mag
siz_nod = 2
var_max = 65535
nod_tn = 5
mem_tn = 7
bc_tn = 2
nl_tn = 2
mem_ym = 1.
#適用範囲の確認
if (nod_tn * siz_nod) > (var_max - 1):
print('error:節点数が適用範囲を超えている。nod_tn * siz_nod > var_max -1 ')
if mem_tn > var_max:
print('error:部材数が適用範囲を超えている。mem_tn > var_max')
#'uint16' 0~65535
#numpy配列の宣言
nod_coo = np.zeros((nod_tn, siz_nod), dtype = 'float64')
mem_are = np.zeros(mem_tn, dtype = 'float64')
mem_nn = np.zeros((mem_tn, siz_nod), dtype = 'uint16')
bc_nn = np.zeros(bc_tn, dtype = 'uint16')
bc_ff = np.zeros((bc_tn, siz_nod), dtype = 'bool')
nl_nn = np.zeros(nl_tn, dtype = 'uint16')
nl_mag = np.zeros((nl_tn, siz_nod), dtype = 'float64')
nod_coo[:] = [[0., 0.],
[100., 100.],
[200., 0.],
[300., 100.],
[400., 0.]]
mem_are[:] = 100.
mem_nn[:] = [[0, 1],
[1, 2],
[2, 3],
[3, 4],
[0, 2],
[2, 4],
[1, 3]]
bc_nn = [0, 4]
bc_ff[:] = [[0, 0],
[1, 0]]
nl_nn[:] = [1, 3]
nl_mag[:] = [[0., -3.],
[0., -3.]]
def output_data():
'''入力データの出力
output_data: [OUTPUT][DATA]
'''
#関数への入力
global siz_nod, mem_ym, nod_tn, nod_coo
global mem_tn, mem_nn, bc_tn, bc_nn, bc_ff
global nl_tn, nl_nn, nl_mag
print('========================================')
print('1.入力データ')
print('(1) 制御データ')
print(' siz_nod, var_max:[{}, {}]'.format(siz_nod, var_max))
print('(2) 共通データ')
print(' E:[{}]'.format(mem_ym))
print('(3) 節点座標')
print(' 節点数:{}'.format(nod_tn))
for i_nn in range(nod_tn):
print('{:4d}: [x:{:12.5f}, y:{:12.5f}]'\
.format(i_nn, nod_coo[i_nn, 0], nod_coo[i_nn, 1]))
print('(4) 部材')
print(' 部材数:{}'.format(mem_tn))
for i_mn in range(mem_tn):
print('{:4d}: (node:{:4d} -- {:4d}), [A:{:12.5f}]'\
.format(i_mn, mem_nn[i_mn, 0], mem_nn[i_mn, 1], mem_are[i_mn]))
print('(5) 境界条件')
print(' 境界条件を与える節点の数:{}'.format(bc_tn))
print(' [境界条件:fix:0, free:1]')
for i_bcn in range(bc_tn):
print('{:4d}: (node:{:4d}), [{:2d}, {:2d}]'\
.format(i_bcn, bc_nn[i_bcn], bc_ff[i_bcn, 0], bc_ff[i_bcn, 1]))
print('(6) 外力')
print(' 外力が作用する節点の数:{}'.format(nl_tn))
for i_nln in range(nl_tn):
print('{:4d}: (node:{:4d}), [x:{:12.5f}, y:{:12.5f}]'\
.format(i_nln, nl_nn[i_nln], nl_mag[i_nln, 0], nl_mag[i_nln, 1]))
def bc_index(siz_nod, var_max, nod_tn, bc_tn, bc_nn, bc_ff):
'''計算準備データの生成
bc_index: [Boundary Condition][INDEX]
(1) global変数として結果を受け渡し
siz_tot:節点の全自由度の総数 (= 節点数(nod_tn) * 自由度(siz_nod))
siz_fix:全自由度の中で境界条件がfixの部分の数
siz_fre:全自由度の中で境界条件がfreeの部分の数
ind_fre[siz_tot → siz_fre]:free部分の通し番号と節点番号の対応表
ind_fix[siz_fix]:fix部分の通し番号と節点番号の対応表
'''
#関数からの出力
global siz_tot, siz_fre, siz_fix, ind_fre, ind_fix
siz_tot = nod_tn * siz_nod
if siz_tot >= var_max:
print('節点数が制限値を超えている')
siz_fix = 0
for i_bcn in range(bc_tn):
for j_dof in range(siz_nod):
if bc_ff[i_bcn, j_dof] == 0:
siz_fix += 1
siz_fre = siz_tot - siz_fix
ind_fre = np.arange(siz_tot, dtype = 'uint16')
ind_fix = np.zeros(siz_fix, dtype = 'uint16')
#fixの部分をvar_maxに入れ替え
for i_bcn in range(bc_tn):
ind_1st = bc_nn[i_bcn] * siz_nod
for j_dof in range(siz_nod):
if bc_ff[i_bcn, j_dof] == 0:
ind_fre[ind_1st + j_dof] = var_max
#fixの部分を除き、前につめる。[0~mm]の範囲が必要なデータ
tmp_fix = 0
tmp_fre = 0
for i in range(siz_tot):
if ind_fre[i] == var_max:
ind_fix[tmp_fix] = i
tmp_fix += 1
else:
ind_fre[tmp_fre] = ind_fre[i]
tmp_fre += 1
def ek_global(i_g_mn, mem_nn, nod_coo, mem_ym, mem_are):
'''i_g_mn番目の要素の全体座標系要素剛性マトリクスの生成
ek_global: [Element K(stiffness matrix)][GLObal coordinate system]
(1) return
ek_glo[4, 4]:全体座標系要素剛性マトリクス, dtype = 'float64'
'''
ek_loc = np.zeros((2, 2), dtype = 'float64')
mem_len, mem_rot = mem_len_rotation(i_g_mn, mem_nn, nod_coo)
#部材座標系要素剛性マトリクス
ek_loc[0, 0] = mem_ym * mem_are[i_g_mn] / mem_len
ek_loc[0, 1] = - ek_loc[0, 0]
ek_loc[1, 0] = ek_loc[0, 1]
ek_loc[1, 1] = ek_loc[0, 0]
#全体座標系要素剛性マトリクス
ek_glo = np.dot(mem_rot.T, np.dot(ek_loc, mem_rot))
return ek_glo
def mem_len_rotation(i_g_mn, mem_nn, nod_coo):
'''mem_nn[i_g_mn]の部材長、[[c,s,0,0],[0,0,c,s]]の算定
mem_len_rotation: [member][LENgth][ROTATION]
(1) return
mem_len: 部材長
mem_rot: 部材座標系に変換する回転行列
[[cos(θ), sin(θ), 0, 0],
[0, 0, cos(θ), sin(θ)]]
(全体座標系における部材の傾きをθとする。反時計回りを正。)
'''
mem_rot = np.zeros((2,4), dtype ='float64')
mem_0_nn = mem_nn[i_g_mn, 0]
mem_1_nn = mem_nn[i_g_mn, 1]
dif_x = nod_coo[mem_1_nn, 0] - nod_coo[mem_0_nn, 0]
dif_y = nod_coo[mem_1_nn, 1] - nod_coo[mem_0_nn, 1]
mem_len = np.sqrt(dif_x * dif_x + dif_y * dif_y)
c = dif_x / mem_len
s = dif_y / mem_len
#mem_rot[:] = [[c, s, 0., 0.], [0., 0., c, s]]
mem_rot[0, 0] = c
mem_rot[1, 2] = c
mem_rot[0, 1] = s
mem_rot[1, 3] = s
return mem_len, mem_rot
def set_gk(i_g_mn, siz_nod, ek_glo, mem_nn, gk):
'''要素剛性マトリクスから全体剛性マトリクスの生成(fix,freeを含む)
set_gk: [SET][Globally assembled K(stiffness matrix)]
(1) return
gk[siz_tot, siz_tot]:全体剛性マトリクス(fix,freeを含む)
'''
be_tn = 2
for i_ben in range(be_tn):
gk_row_1st = mem_nn[i_g_mn, i_ben] * siz_nod
ek_row_1st = i_ben * siz_nod
for j_ben in range(be_tn):
gk_col_1st = siz_nod * mem_nn[i_g_mn, j_ben]
ek_col_1st = siz_nod * j_ben
for k_dof in range(siz_nod):
gk_row = gk_row_1st + k_dof
ek_row = ek_row_1st + k_dof
for l_dof in range(siz_nod):
gk_col = gk_col_1st + l_dof
ek_col = ek_col_1st + l_dof
gk[gk_row, gk_col] += ek_glo[ek_row, ek_col]
return gk
def set_nodal_load(siz_nod, siz_tot, nl_tn, nl_nn, nl_mag):
'''荷重ベクトルの生成(fix,freeを含む)
set_nodal_load: [SET][NODAL][LOAD]
(1) return
nl_v[siz_tot]:荷重ベクトル
'''
nl_v = np.zeros(siz_tot, dtype = 'float64')
if nl_tn != 0:
for i_nln in range(nl_tn):
nl_1st = siz_nod * nl_nn[i_nln]
for j_dof in range(siz_nod):
nl_v[nl_1st + j_dof] += nl_mag[i_nln, j_dof]
return nl_v
def gk_reaction_force(siz_tot, siz_fre, siz_fix, ind_fre, ind_fix, gk):
'''反力算定用の剛性マトリクス
gk_reaction_force:[Globally assembled K(stiffness matrix)][REACTION][FORCE]
全体剛性マトリクスgkのfix行、free列を抜き出し、gk_rfに代入(反力算定用)
(1) return
gk_rf[siz_fix, siz_fre]:
反力計算要に全体剛性マトリクスgk[siz_tot, siz_tot]から必要部分を抜き出す。
行方向はfix部分のみ抜き出し、列方向はfree部分のみ抜き出す。
'''
gk_rf = np.zeros((siz_fix, siz_fre), dtype = 'float64')
for i_fix in range(siz_fix):
gk_row_fix = ind_fix[i_fix]
for j_fre in range(siz_fre):
gk_col_fre = ind_fre[j_fre]
gk_rf[i_fix, j_fre] = gk[gk_row_fix, gk_col_fre]
return gk_rf
def del_fix_gk_nl(siz_tot, siz_fre, ind_fre ,nl_v, gk):
'''gk[,], nl_v[]のfix部分を削除し、free部分を前に寄せる。
del_fix_gk_nl: [DELete][FIX][Globally assembled K(stiffness matrix)]
[Nodal Load]
(1) return
nl_v[siz_tot → siz_fre]:荷重ベクトル(fix部削除)
gk[siz_tot → siz_fre, siz_tot → siz_fre]:
全体座標系剛性マトリクス(fix部削除)
※注意:fix部分のデータを削除しfree部分のデータを前に寄せているので、
siz_freより後のデータは不要。
行列計算をするときはスライスでfree部分のみを抜き出す必要あり。
'''
for i_fre in range(siz_fre):
gk_row_fre = ind_fre[i_fre]
nl_v[i_fre] = nl_v[gk_row_fre]
for j_fre in range(siz_fre):
gk_col_fre = ind_fre[j_fre]
gk[i_fre, j_fre] = gk[gk_row_fre, gk_col_fre]
return nl_v, gk
def node_displacement(siz_nod, nod_tn, siz_fre, ind_fre, dis_fre_v):
'''x, y方向変位から変位の大きさを求め、nod_dis[i, j]に代入
node_displacement: [NODE][DISPLACEMENT]
(1) return
nod_dis[i, j]:i節点のj方向の変位
(j=0:x方向変位, j=1:y方向変位, j=2:x,y方向を考慮した変位の大きさ)
'''
nod_dis = np.zeros((nod_tn, siz_nod + 1), dtype = 'float64')
for i_fre in range(siz_fre):
nn = ind_fre[i_fre] // siz_nod
dof = ind_fre[i_fre] % siz_nod
nod_dis[nn, dof] = dis_fre_v[i_fre]
for i_nn in range(nod_tn):
nod_dis_x = nod_dis[i_nn, 0]
nod_dis_y = nod_dis[i_nn, 1]
nod_dis[i_nn, 2] = np.sqrt(nod_dis_x ** 2 + nod_dis_y ** 2)
return nod_dis
def stress(mem_tn, siz_nod, mem_nn, nod_coo, nod_dis):
'''部材軸力の計算
stress: [STRESS]
(1) return
mem_str[i]:i部材の軸力(引張側正)
'''
be_tn = 2
dis_be_glo = np.zeros(be_tn * siz_nod, dtype = 'float64')
mem_str = np.zeros(mem_tn, dtype = 'float64')
for i_mn in range(mem_tn):
mem_len, mem_rot = mem_len_rotation(i_mn, mem_nn, nod_coo)
for j_ben in range(be_tn):
dis_1st = j_ben * siz_nod
for k_dof in range(siz_nod):
dis_be_glo[dis_1st + k_dof] = nod_dis[mem_nn[i_mn, j_ben], k_dof]
dis_be_loc = np.dot(mem_rot, dis_be_glo)
mem_str[i_mn] = mem_ym * mem_are[i_mn] / mem_len \
* (dis_be_loc[1] - dis_be_loc[0])
return mem_str
def reaction_force(siz_fix, ind_fix, gk_rf, dis_fre_v):
'''反力の計算
reaction_force: [REACTION][FORCE]
(1) return
rf_v[siz_fix]:反力 (i:反力の通し番号)
rf_nn[siz_fix]:反力の通し番号に対応する反力の節点番号 ※リスト
rf_der[siz_fix]:反力の通し番号に対応する反力の方向の記号 ※リスト
'''
rf_v = np.dot(gk_rf, dis_fre_v)
rf_nn = []
rf_der = []
for i_fix in range(siz_fix):
rf_nn.append(ind_fix[i_fix] // siz_nod)
if (ind_fix[i_fix] % siz_nod) == 0:
rf_der.append('x')
else:
rf_der.append('y')
return rf_v, rf_nn, rf_der
def output_result():
'''計算結果の出力
output_result: [OUTPUT][RESULT]
誤差確認のためfloatの出力は書式指定せず
'''
#関数への入力
global nod_tn, nod_dis, mem_tn, mem_nn, mem_str
global siz_fix, rf_nn, rf_der, rf_v
print('========================================')
print('2.計算結果')
print('(1) 節点変位')
print(' 節点: 変位[x:], [y:], [xy:]')
for i_nn in range(nod_tn):
print('{:4d}: [x:{}], [y:{}], [xy:{}]'\
.format(i_nn, nod_dis[i_nn, 0], nod_dis[i_nn, 1], nod_dis[i_nn, 2]))
print('(2) 部材応力')
print(' 部材: (節点0--節点1), 部材応力')
for i_mn in range(mem_tn):
print('{:4d}: ({:4d} -- {:4d}), {}'\
.format(i_mn, mem_nn[i_mn, 0], mem_nn[i_mn, 1], mem_str[i_mn]))
print('(3) 反力')
print(' No.:(節点-方向), 反力')
for i_fix in range(siz_fix):
print('{:4d}:({:4d} - {}), {}'\
.format(i_fix, rf_nn[i_fix], rf_der[i_fix], rf_v[i_fix]))
if __name__ == '__main__':
'''メインプログラム
(1) 入力、計算準備データ
input_data(), bc_index() にて
(2) 主な計算用データ
gk[siz_tot→nfree]:全体剛性マトリクス ※def del_fix_gk_nl()前後で使用範囲が変わる
nl_v[siz_tot→nfree]:荷重ベクトル ※def del_fix_gk_nl()前後で使用範囲が変わる
ek_loc[2, 2]:要素剛性マトリクス(部材座標系)
ek_glo[4, 4]:要素剛性マトリクス(全体座標系)
gk_rf[siz_fix, siz_fre]:反力算定用の剛性マトリクス(fix行、free列の抜き出し)
dis_fre_v[siz_fre]:節点変位のベクトル(freeの部分)
(3) 計算結果
nod_dis[nod_tn]:節点変位のベクトル(free,fix)
mem_str[mem_tn]:部材応力
rf_v[siz_fix]:反力
rf_nn_der[siz_fix][i]:反力の節点番号と方向(i=0:節点番号、i=1:方向) ※リスト
'''
#データ入力
input_data_1()
#input_data_2() #入力データ例2を計算する場合は、こちらに切り替える。
#入力データの出力
output_data()
#計算準備データ
#global siz_tot, siz_fre, siz_fix, ind_fre, ind_fix
bc_index(siz_nod, var_max, nod_tn, bc_tn, bc_nn, bc_ff)
gk = np.zeros((siz_tot, siz_tot), dtype = 'float64')
for i_g_mn in range(mem_tn):
#全体座標系要素剛性マトリクスの生成
ek_glo = ek_global(i_g_mn, mem_nn, nod_coo, mem_ym, mem_are)
#要素剛性マトリクスより全体剛性マトリクスを生成
gk = set_gk(i_g_mn, siz_nod, ek_glo, mem_nn, gk)
#荷重ベクトルの生成
nl_v = set_nodal_load(siz_nod, siz_tot, nl_tn, nl_nn, nl_mag)
#fixされているところの剛性マトリクスのみを抽出(反力算定用)
gk_rf = gk_reaction_force(siz_tot, siz_fre, siz_fix, ind_fre, ind_fix, gk)
#gk[,], nl_v[]のfix部分を削除し、free部分を前に寄せる。
nl_v, gk = del_fix_gk_nl(siz_tot, siz_fre, ind_fre, nl_v, gk)
#連立一次方程式を解き、拘束条件のない部分の変位を求める
dis_fre_v = np.linalg.solve(gk[0:siz_fre, 0:siz_fre], nl_v[0:siz_fre])
#節点変位の計算
nod_dis = node_displacement(siz_nod, nod_tn, siz_fre, ind_fre, dis_fre_v)
#部材応力の計算
mem_str = stress(mem_tn, siz_nod, mem_nn, nod_coo, nod_dis)
#反力の計算
rf_v, rf_nn, rf_der =reaction_force(siz_fix, ind_fix, gk_rf, dis_fre_v)
#計算結果の出力
output_result()3.解析モデルと解析結果
平面トラス解析プログラムのサンプルコードでは、コードの中でdef input_data_1()、def input_data_2()の2種類の解析モデルを紹介しています。
(1) 解析モデル1
def input_data_1()に示す解析モデルと解析結果です。
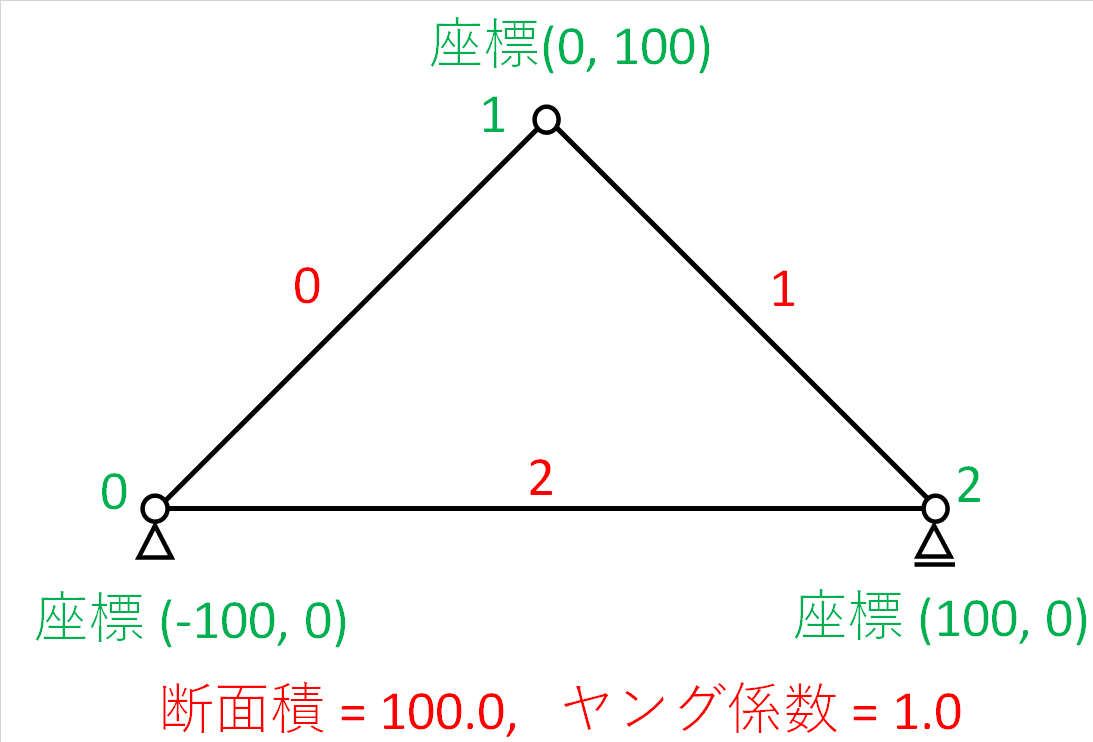
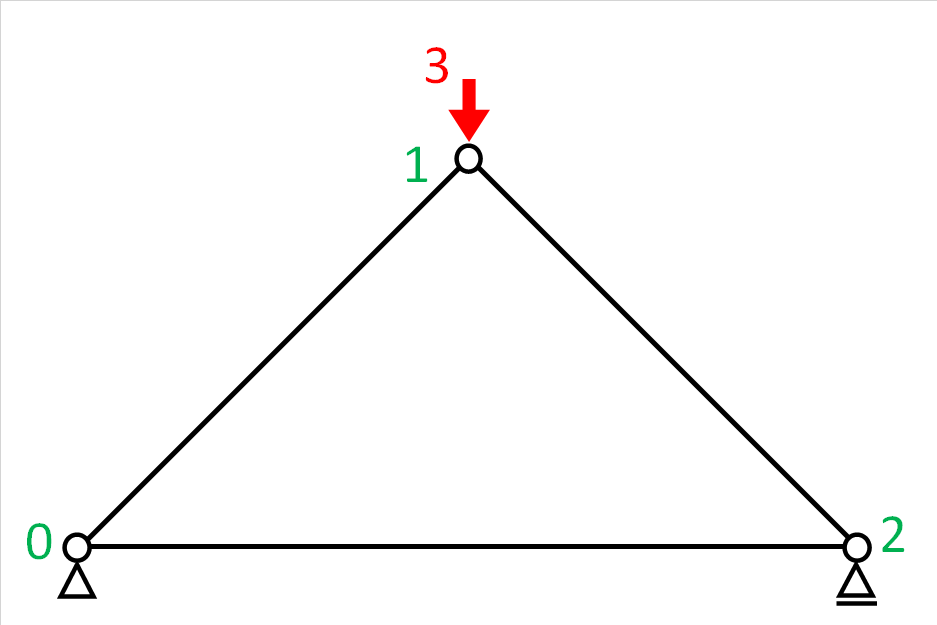
以下、出力結果です。節点変位の「xy:」とはx方向変位とy方向変位から求めた合成変位(二乗和平方根)です。
#出力02
========================================
1.入力データ
(1) 制御データ
ndim, uint_max:[2, 65535]
(2) 共通データ
E:[1.0]
(3) 節点座標
節点数:3
0: [x: -100.00000, y: 0.00000]
1: [x: 0.00000, y: 100.00000]
2: [x: 100.00000, y: 0.00000]
(4) 部材
部材数:3
0: (node: 0 -- 1), [A: 100.00000]
1: (node: 1 -- 2), [A: 100.00000]
2: (node: 0 -- 2), [A: 100.00000]
(5) 境界条件
境界条件を与える節点の数:2
[境界条件:fix:0, free:1]
0: (node: 2), [ 1, 0]
1: (node: 0), [ 0, 0]
(6) 外力
外力が作用する節点の数:1
0: (node: 1), [x: 0.00000, y: -3.00000]
========================================
2.計算結果
(1) 節点変位
節点: 変位[x:], [y:], [xy:]
0: [x:0.0], [y:0.0], [xy:0.0]
1: [x:1.5], [y:-5.7426406871192865], [xy:5.935311454452738]
2: [x:3.0], [y:0.0], [xy:3.0]
(2) 部材応力
部材: (節点0--節点1), 部材応力
0: ( 0 -- 1), -2.1213203435596433
1: ( 1 -- 2), -2.121320343559643
2: ( 0 -- 2), 1.5
(3) 反力
No.:(節点-方向), 反力
0:( 0 - x), 0.0
1:( 0 - y), 1.5
2:( 2 - y), 1.5(2) 解析モデル2
def input_data_2()に示す解析モデルと解析結果です。
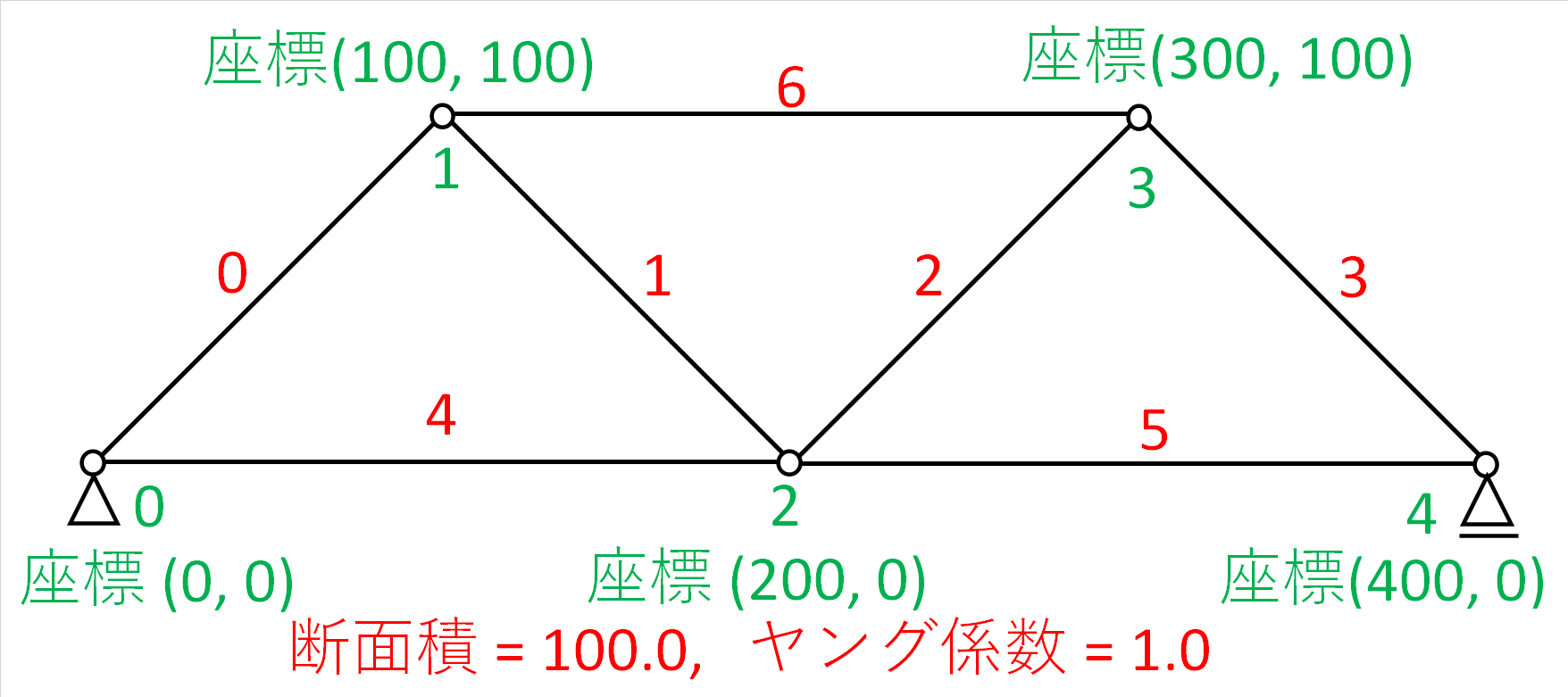
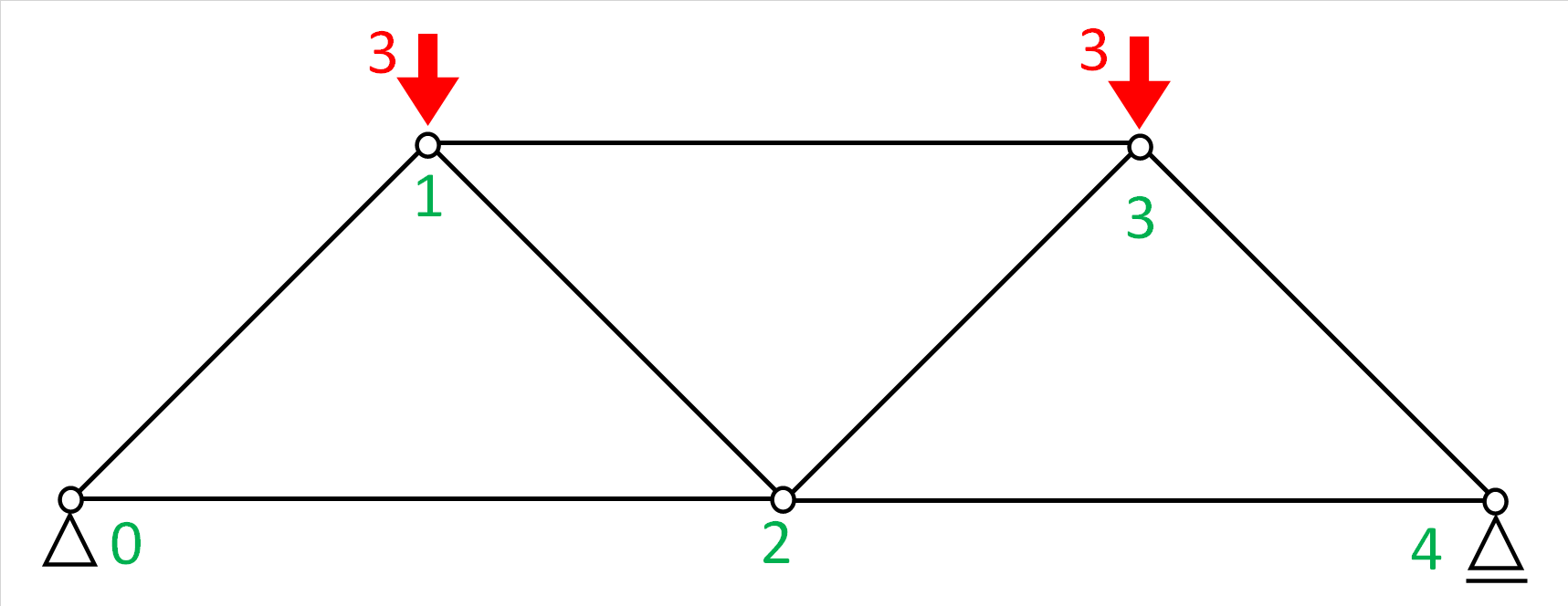
#出力02
========================================
1.入力データ
(1) 制御データ
ndim, uint_max:[2, 65535]
(2) 共通データ
E:[1.0]
(3) 節点座標
節点数:5
0: [x: 0.00000, y: 0.00000]
1: [x: 100.00000, y: 100.00000]
2: [x: 200.00000, y: 0.00000]
3: [x: 300.00000, y: 100.00000]
4: [x: 400.00000, y: 0.00000]
(4) 部材
部材数:7
0: (node: 0 -- 1), [A: 100.00000]
1: (node: 1 -- 2), [A: 100.00000]
2: (node: 2 -- 3), [A: 100.00000]
3: (node: 3 -- 4), [A: 100.00000]
4: (node: 0 -- 2), [A: 100.00000]
5: (node: 2 -- 4), [A: 100.00000]
6: (node: 1 -- 3), [A: 100.00000]
(5) 境界条件
境界条件を与える節点の数:2
[境界条件:fix:0, free:1]
0: (node: 0), [ 0, 0]
1: (node: 4), [ 1, 0]
(6) 外力
外力が作用する節点の数:2
0: (node: 1), [x: 0.00000, y: -3.00000]
1: (node: 3), [x: 0.00000, y: -3.00000]
========================================
2.計算結果
(1) 節点変位
節点: 変位[x:], [y:], [xy:]
0: [x:0.0], [y:0.0], [xy:0.0]
1: [x:8.999999999999996], [y:-17.485281374238568], [xy:19.665580711901036]
2: [x:5.999999999999996], [y:-20.48528137423857], [xy:21.345883747967093]
3: [x:2.999999999999996], [y:-17.48528137423857], [xy:17.7407740737628]
4: [x:11.999999999999995], [y:0.0], [xy:11.999999999999995]
(2) 部材応力
部材: (節点0--節点1), 部材応力
0: ( 0 -- 1), -4.242640687119284
1: ( 1 -- 2), 2.51214793389404e-15
2: ( 2 -- 3), 0.0
3: ( 3 -- 4), -4.2426406871192865
4: ( 0 -- 2), 2.999999999999998
5: ( 2 -- 4), 2.9999999999999996
6: ( 1 -- 3), -3.0
(3) 反力
No.:(節点-方向), 反力
0:( 0 - x), 1.3322676295501878e-15
1:( 0 - y), 2.999999999999999
2:( 4 - y), 3.04.改訂履歴
以下、改訂履歴です。2021.2.11にVer.1.04に改訂しました。変数名を全面改定するなど大幅な見直しを行いました。
改訂履歴の表示・非表示の切り替え
※ブラウザによっては最初から表示されてしまいます。(Google Chrome推奨)
(2019.11.19) Ver.1.01
プロトタイプ
(2020.3.9) Ver.1.02
Ver.1.01:共通
Numpy配列の表記をa[i][j]タイプからa[i, j]タイプに変更
Ver.1.01:44行目
ndimの部分はディメンジョンを表すものではないため2とする
indv = np.zeros((nel, ndim), dtype = 'uint16')
→indv = np.zeros((nel, 2), dtype = 'uint16')
Ver.1.01:194行目
ek_global = np.zeros((4, 4), dtype = 'float64')
→不要
Ver.1.01:223, 224行目
rotation[:] = [[c, s, 0., 0.],
[0., 0., c, s]]
→速度重視
rotation[0, 0] = c
rotation[1, 2] = c
rotation[0, 1] = s
rotation[1, 3] = s
Ver.1.01:249行目
return gk
→削除
Ver.1.01:369行目
print(' 部材: (節点1--節点2), 部材応力')
→print(' 部材: (節点0--節点1), 部材応力')
(2020.3.11) Ver.1.03
Ver.1.02:230~250行目
def set_stiff()のgkを関数内でglobal宣言
→引数でgkを渡し、returnでgkを返す。
Ver.1.02:412行目
set_stiff(iii, ek_global, indv)
→gk = set_stiff(iii, ek_global, indv, gk)
Ver.1.02:281~299行目
def del_stiff_fix()のf_load, gkを関数内でglobal宣言
→引数でf_load, gkを渡し、returnでf_load, gkを返す。
Ver.1.02:412行目
del_stiff_fix(nmat, n_free, ind_free)
→f_load, gk = del_stiff_fix(nmat, n_free, ind_free, f_load, gk)
(2021.2.11) Ver.1.04
変数名の全面改定
def output_datum(), def output_result()において参照する
変数の数が多いため、global宣言を省略していたが、
global宣言を行い、def関数の外から参照したデータを明示した。
def bc_index()において、以下のコードにより
gk[,], nl_v[]のfix部分を削除していたが、
ind_fre = np.delete(ind_fre, slice(siz_fre, siz_tot), 0)
計算速度向上のため、配列の大きさはそのままとしfree部分を前に寄せた。
なお、後ろに残ったデータは意味のないデータとして無視する。
連立一次方程式の計算では、計算する部分をスライスで指定する。
def set_stiff()において、引数dim_nを追加。
1行に記述できる文字数を増やすためにインデントを
半角4文字から半角2文字に変更
input_dataに、節点数や部材数の適用範囲を確認する行を追加。
5.関連記事
以下、平面トラスの有限要素法サンプルコードの解説記事です。
私が実際に購入した教材のご紹介
以下、私が実際に購入したPythonの教材をまとめてみました。 Pythonを学習する上で、少しでもお役に立つことができればうれしいです。
・Python♪私が購入したPythonの書籍のレビュー
・UdemyのPythonの動画講座を書籍を買う感覚で購入してみた
その他
液晶ペンタブレットを買いました
(1) モバイルディスプレイを買うつもりだったのに激安ペンタブレット購入
以下、私が光回線を導入した時の記事一覧です。
(1) 2020年「光回線は値段で選ぶ」では後悔する ←宅内工事の状況も説明しています。
(2) NURO光の開通までWiFiルーターを格安レンタルできる
(3) NURO光の屋外工事の状況をご紹介。その日に開通!
(4) 光回線開通!実測するとNURO光はやっぱり速かった
(5) ネット上のNURO光紹介特典は個人情報がもれないの?

