行列の積や転置行列についてNumpyの関数を使えば簡単ですが、関数を使わない方法も紹介します。PythonのFEMの書籍はまだ少ないため、CやFORTRANのコードを読むときに役に立ちます。熟語を覚えるような感覚でコードを覚えれば簡単です。
0. FEMなど数値解析シリーズ
この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。
1.行列の積
X=ABという行列の積を考えてみます。例としてAは3行3列、Bは3行2列です。行数、列数は1から始まりますが、Pythonのfor文が0から始まることを考慮して、添え字を00から始めています。
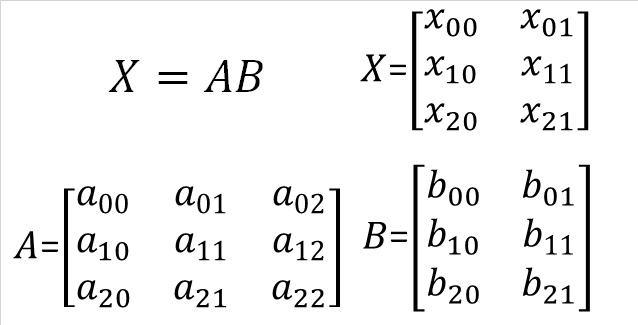
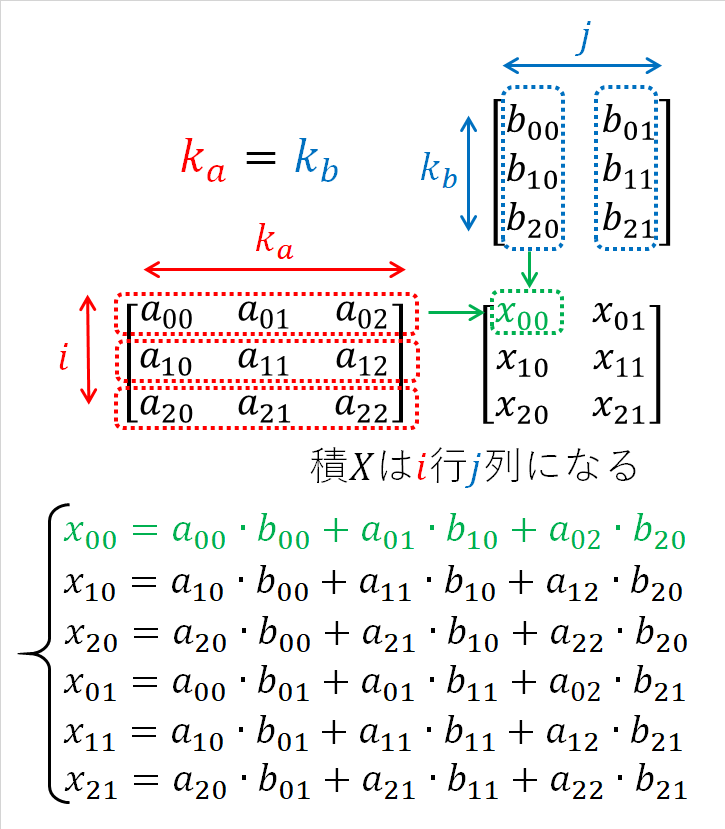
慣れない方は以下のような図で計算をイメージするとわかりやすいです。図のポイントは以下の通りです。
- 行列の計算では下図のkaとkbの大きさは同じです。赤や青の点線で囲った部分同士の内積を求めるのですから、同じ長さでなければ計算できません。
- 図下側の計算式をを参考に、AやBのどの位置のベクトルを使うのか確認してください。
- 計算結果である行列Xの行数、列数はそれぞれi行、j列となります。
コード01は、X= ABの行列の積の計算例です。11行目の.dot()を使えば行列計算も1行で終了です。Pythonはfor文の処理が遅いので、行列処理はできるだけnumpyの関数を使うべきです。
#コード01
import numpy as np
a = np.array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]])
b = np.array([[0., 1.],
[2., 3.],
[4., 5.]])
x = np.dot(a, b)
print(x)#出力01
[[10. 13.]
[28. 40.]
[46. 67.]]コード02はnumpyの関数を使わない方法です。15~18行目がx = np.dot(a, b)に相当する部分です。この部分のコードは熟語を覚えるようなつもりでコードを覚えておいても損はありません。Pythonでは使うことはないかもしれませんが、他のプログラム言語ででこの形を見たときに、行列の積であるとわかれば読みやすくなります。
#コード02
import numpy as np
a = np.array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]])
b = np.array([[0., 1.],
[2., 3.],
[4., 5.]])
x = np.zeros((3, 2))
ii = 3
kk = 3
jj = 2
for i in range(ii):
for j in range(jj):
for k in range(kk):
x[i][j] = x[i][j] + a[i][k] * b[k][j]
print(x)#出力02
[[10. 13.]
[28. 40.]
[46. 67.]]2.行列、ベクトルの積と内積
コード03は1行3列の行列と、3行1列の行列の積です。出力03のように両側を[ ]で囲まれた[14.]が出力されます。
#コード03
import numpy as np
a = np.array([0., 1., 2.])
b = np.array([[3.],
[4.],
[5.]])
x = np.dot(a, b)
print(x)#出力03
[14.]だたし、numpyのdot関数では、コード04のようにベクトルの内積を求めることもできます。行列計算であれば、aの行数とbの列数が異なるので計算できないことになりますが、エラーにはならず内積が求められます。dot関数では要素数が同じ1次元配列同士の計算では行列の積ではなく内積が計算されます。出力04のように両側に[ ]はなく、14.0という値が出力されます。
#コード04
import numpy as np
a = np.array([0., 1., 2.])
b = np.array([3., 4., 5.])
x = np.dot(a, b)
print(x)#出力04
14.0なお、書籍やサイトで「行列の積」を「行列の内積」と表現しているケースが散見されますので注意してください。内積は対応する成分の積の全ての和のことであり1つの値となります。また、式も積はX=AB、内積はX=A・Bです。
例えば「ゼロから作るでDeep Learning」でも初版第8刷で「3.3.2 行列の内積」となっていますが、これは「内積」ではなく「積」です。
3.転置行列
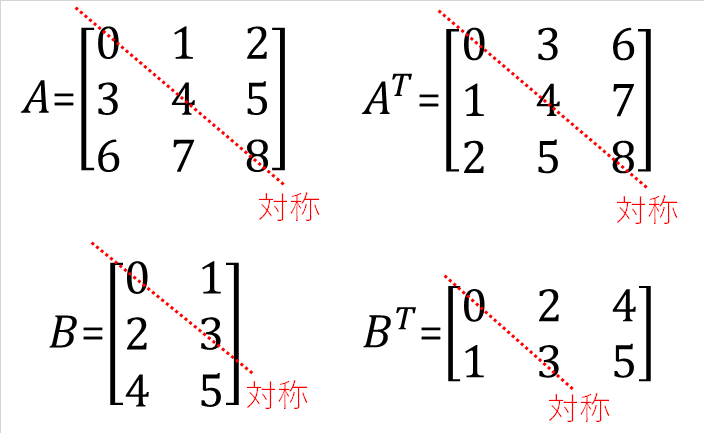
転置行列は行と列を入れ替えた行列であり、下図のようになります。
転置行列は行と列を入れ替えた行列であり、下図のようになります。行列A, Bの転置行列がそれぞれAT, BTです。赤色の点線でひっくりかえしたような行列になります。
では、実際に下図の計算を行い、行列XをPythonで求めてみましょう。
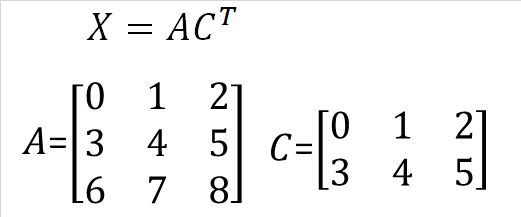
コード05はnumpyの.Tメソッドを使った計算方法です。10行目でcの転置行列としてc.Tを用いています。
#コード05
import numpy as np
a = np.array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]])
c = np.array([[0., 2., 4.],
[1., 3., 5.]])
x = np.dot(a, c.T)
print(x)#出力05
[[10. 13.]
[28. 40.]
[46. 67.]]コード06はnumpyのメソッドを使わない方法です。17行目をよく見ると、コード02とは異なりc[k][j]ではなく、 c[j][k]となっていることに注目してください。転置行列は行と列の入れ替えなので、jとkを入れ替えているのです。
#コード06
import numpy as np
a = np.array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]])
c = np.array([[0., 2., 4.],
[1., 3., 5.]])
x = np.zeros((3, 2))
ii = 3
kk = 3
jj = 2
for i in range(ii):
for j in range(jj):
for k in range(kk):
x[i][j] = x[i][j] + a[i][k] * c[j][k]
print(x)#出力06
[[10. 13.]
[28. 40.]
[46. 67.]]線形代数の知識としては、「積」「転置行列」「内積」の他にも「逆行列」「単位行列」ぐらいは、その概要を理解しておきましょう。
私が実際に購入した教材のご紹介
以下、私が実際に購入したPythonの教材をまとめてみました。 Pythonを学習する上で、少しでもお役に立つことができればうれしいです。
・Python♪私が購入したPythonの書籍のレビュー
・UdemyのPythonの動画講座を書籍を買う感覚で購入してみた
その他
液晶ペンタブレットを買いました
(1) モバイルディスプレイを買うつもりだったのに激安ペンタブレット購入
以下、私が光回線を導入した時の記事一覧です。
(1) 2020年「光回線は値段で選ぶ」では後悔する ←宅内工事の状況も説明しています。
(2) NURO光の開通までWiFiルーターを格安レンタルできる
(3) NURO光の屋外工事の状況をご紹介。その日に開通!
(4) 光回線開通!実測するとNURO光はやっぱり速かった
(5) ネット上のNURO光紹介特典は個人情報がもれないの?


