全体座標系のZ軸と部材座標系のx軸が平行でない場合の方向余弦の式を求めます。図を見ながら順を追って考えれば、それほど難しい計算ではありません。空間ベクトルの扱い方についても解説しますので、ベクトルの内積や外積が難しいと感じている方も読んでみてください。
理解しにくいところがある場合には、以下の記事を参考にしてください。
Python♪FEM:3次元FEMの右手座標系と右ネジの方向
Python♪FEM:コードアングルを詳しく図解
Python♪FEM:空間ベクトルの外積と内積
0. FEMなど数値解析シリーズ
この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。
1.方向余弦を求めるために使うベクトル
方向余弦は、全体座標系のZ軸と部材座標系のx軸が平行な場合と、平行ではない場合で計算式が異なります。平行ではない場合について考えていきたいと思います。
この記事では平行ではない場合の方向余弦をコードアングルから求めたいと思います。
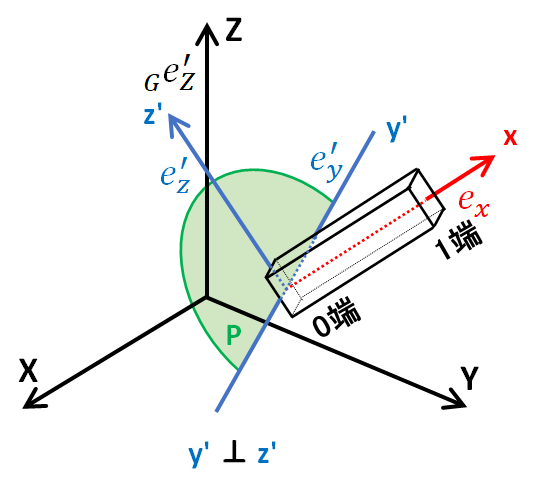
なお、全体座標系X, Y, Z、部材座標系x, y, zと、方向余弦を求めるときに使用するベクトルを下図に示します。どこを示すベクトルかわからなくなったら、下図を参考にしてください。
なお、これらのベクトルの要素は全て全体座標系で表現しますので、以後、座標系を混同しないようにしてください。
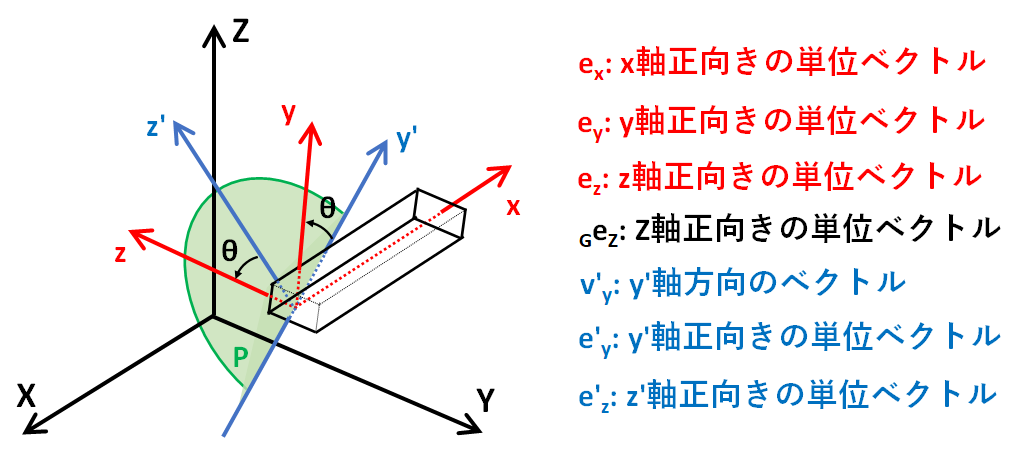
2.方向余弦とは
単位ベクトルexの要素であるlx, mx, nxは部材座標x軸の全体座標軸に対する方向余弦です。
つまり、部材座標系x軸と全体座標系のX, Y, Z軸のなす角をθxX, θxY, θxZとすると、lx = cos(θxX), mx = cos(θxY), nx = cos(θxZ)です。
なお、exは部材座標系のx軸正向きの単位ベクトルを全体座標(lx, mx, nx)で表現したものとも言えます。
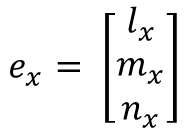
同様に部材座標系y, z軸の全体座標軸に対する方向余弦は、y, z軸正向きの単位ベクトルey =(ly, my, ny),ez=(lz, mz, nz)と表現できます。
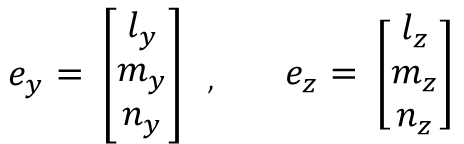
方向余弦を用いれば、全体座標系の座標(GX, GY, GZ)を部材座標系の座標(x, y, z)に変換することができます。
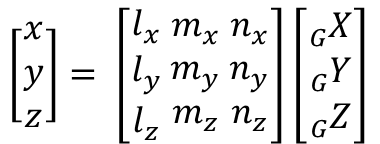
3.部材座標系x軸の全体座標軸に対する方向余弦
それでは、部材座標系x軸の全体座標軸に対する方向余弦exを求めてみましょう。
部材i端の全体座標系の座標を(GXi, GYi, GZi)とすると簡単に求めることができます。余弦(cos)ですから、感覚的にも捉えやすいのではないでしょうか。

4.部材座標系y'軸に平行な単位ベクトル
次にコードアングルが0の場合の部材座標系y'軸の正向きの単位ベクトルe'yを求めたいと思います。
さて、平面Pは、部材0端を通りexを法線ベクトルとする平面です。
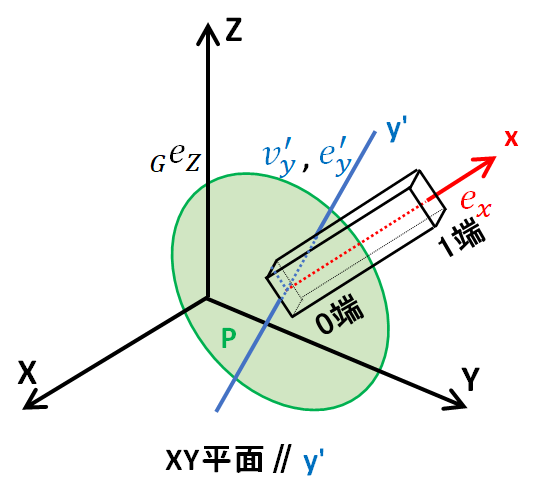
y'軸はXY平面に並行で、0端を通り、平面P上にある直線です。
したがって、y'軸は、x軸(ex)と垂直であり、xy平面の法線ベクトルGeZ(0,0,1)とも垂直です。
つまり、y'軸に平行なベクトルv'yはexとGeZの外積により求めることができます。なお、exとGeZのなす角は90度ではないので、v'yは単位ベクトルではありません。
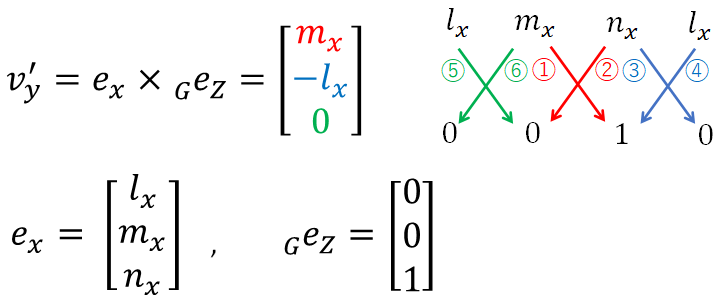
※上式の色は外積計算の順序を示すものなので、他の図の色とは関係がありません。
v'yの長さL'yとすると、y'軸に平行な単位ベクトルe'yはv'y/L'yです。
ただし、z'軸がわからなければ、y'軸の向きが決まりませんのでe'yの向きの決定は後回しにします。
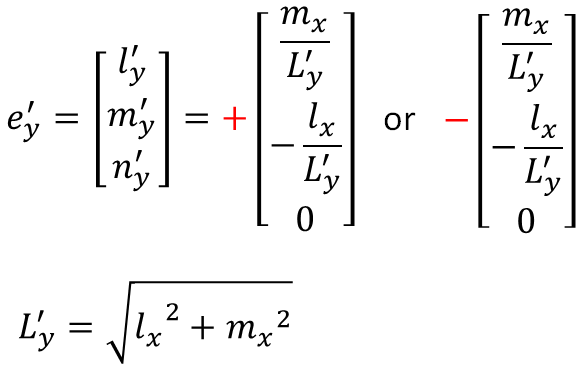
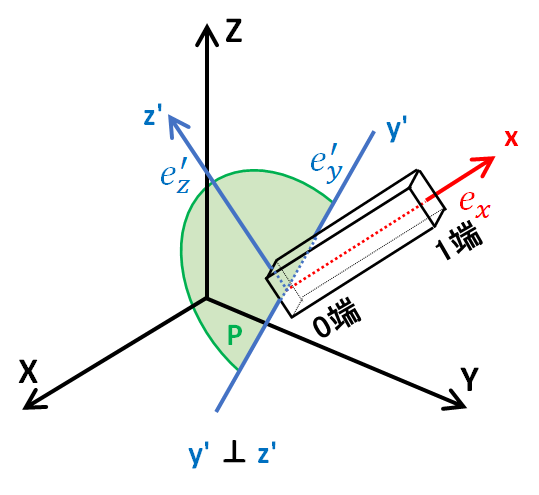
5.部材座標系z'軸に並行な単位ベクトル
次に部材座標系z'軸に並行な単位ベクトルe'zを求めます。e'zはexとe'yに直角なので、e'zはexとe'yの外積で求めることができます。
なお、exとe'yは単位ベクトルであり互いに垂直です。従って、exとe'yの外積を図形的に考えると、外積はexとe'yを隣り合う2辺とする長方形の面積なので、外積e'zの長さは1となります。
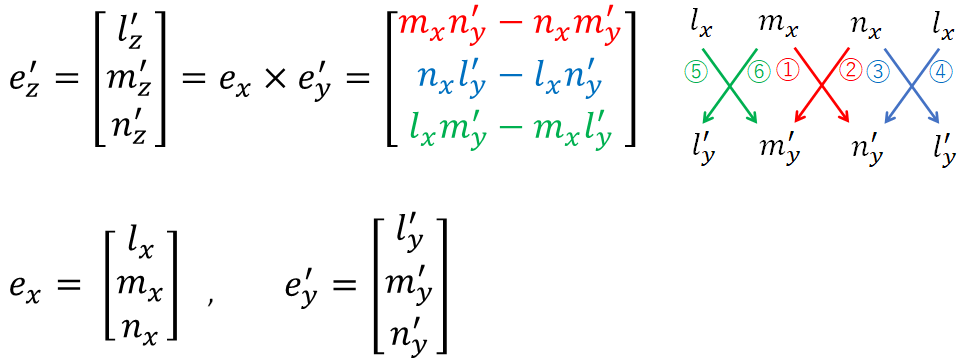
6.部材座標系z'軸の向き
e'zの向きについては、全体座標系のZ軸正向きの単位ベクトルGeZ=(0, 0, 1)とe'zのなす角度が90度より小さい値である必要があります。
つまり、e'zとGeZの内積は0より大きい必要があります。
なお、最初の条件により、全体座標系のZ軸と部材座標系のx軸が平行ではないので、内積が0になることはありません。
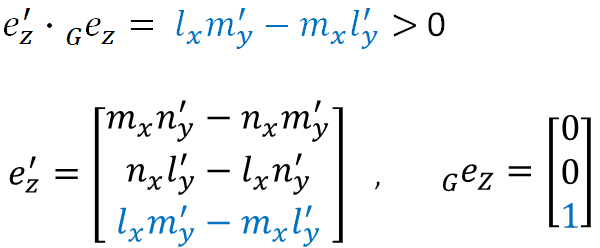
e'zとGeZの内積の正負は、e'yの向きによって変化します。そこで、(l'y, m'y, n'y) = +(mx/L'y, -lx/L'y, 0)と(l'y, m'y, n'y) = ー(mx/L'y, -lx/L'y, 0)をそれぞれ代入して、結果を確認します。
まずは、(l'y, m'y, n'y) = +(mx/L'y, -lx/L'y, 0)を代入してみましょう。以下、代入結果ですが、内積が負の値となり条件をみたすことができません。
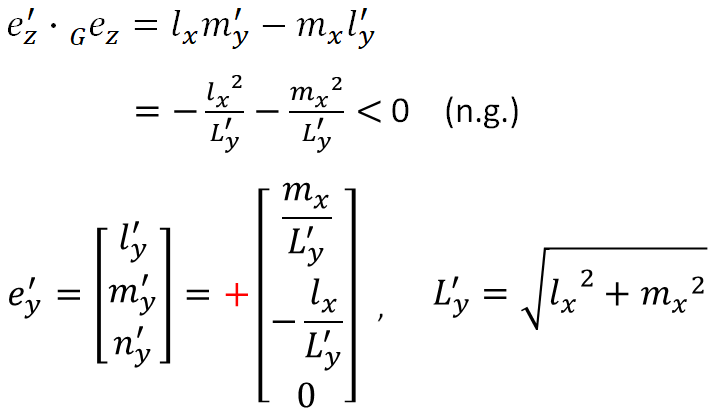
一方、(l'y, m'y, n'y) = ー(mx/L'y, -lx/L'y, 0)を代入すると、内積が正の値となり条件をみたすことができます。
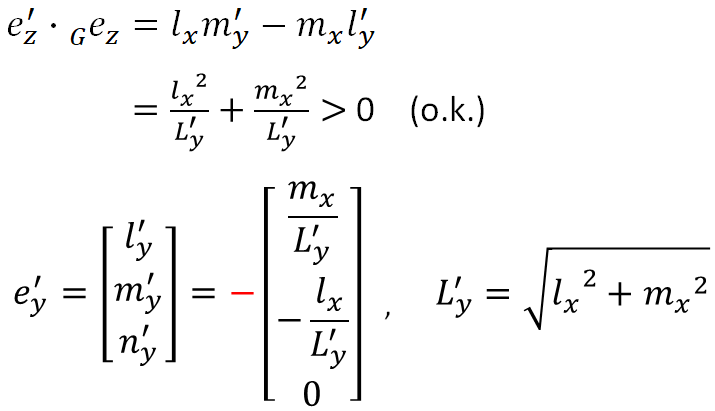
つまり、この結果よりe'yの向きが定まりました。
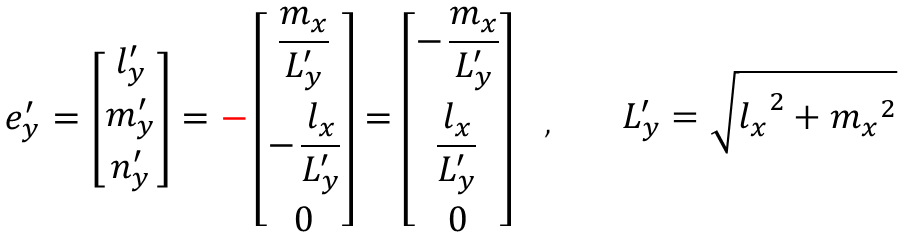
e'yの向きが定まると、e'y=(l'y, m'y, n'y) = (-mx/L'y, lx/L'y, 0)を代入できるので、e'zが定まります。
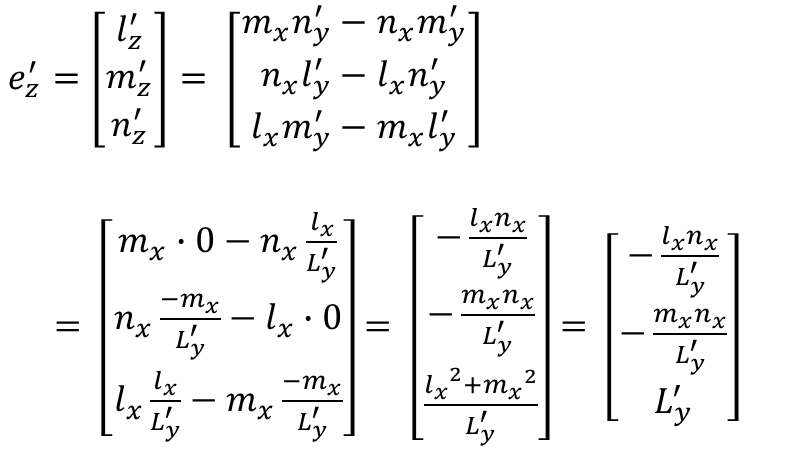
これで、e'y、e'zをexの要素の値を使って求めることができました。
7.部材座標系のx軸を中心に右ねじの方向に回転
最後に部材座標系のx軸を中心に右ねじの方向にθ回転させます。

回転後のy, z軸上の単位ベクトルey, ezは、回転前のe'y, e'z回転させて求めるのではなく、まず、ey, ezをy', z'軸上に分解し、分解したベクトルの和によって求めます。(下図参照)
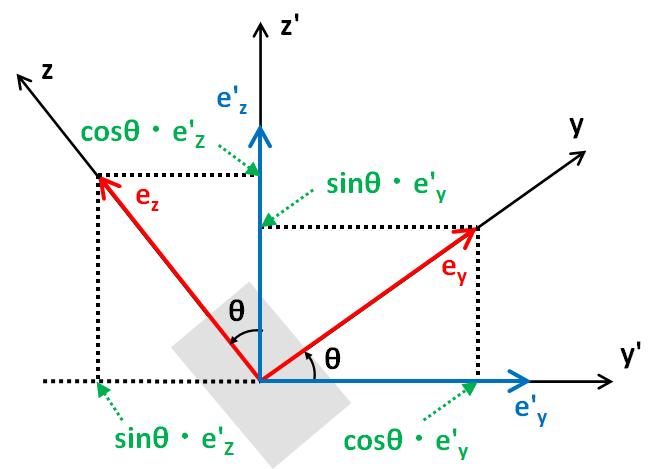
これを式にすると、下式を導くことができます。
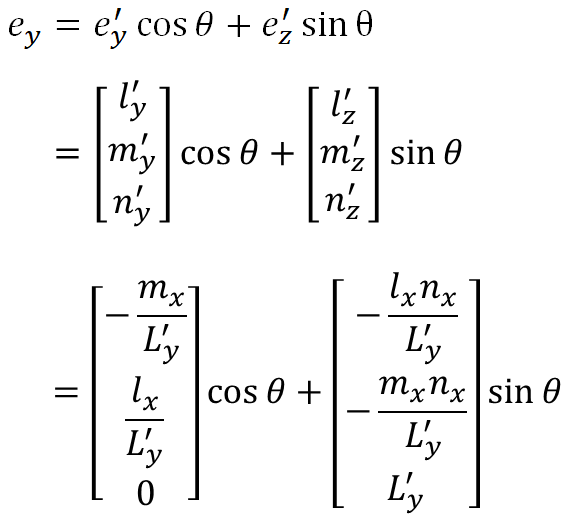
ここで、
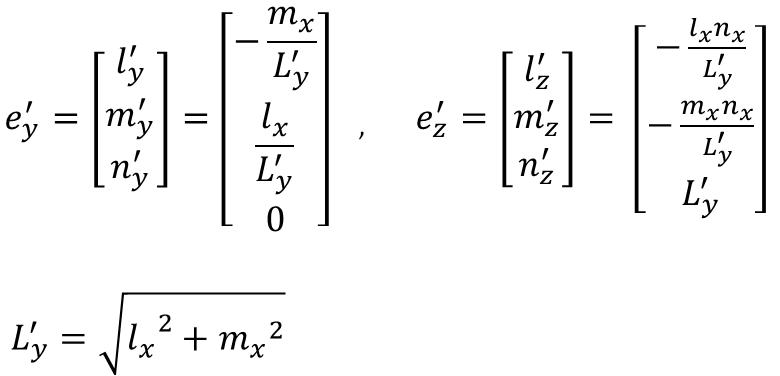
ezについても同様に
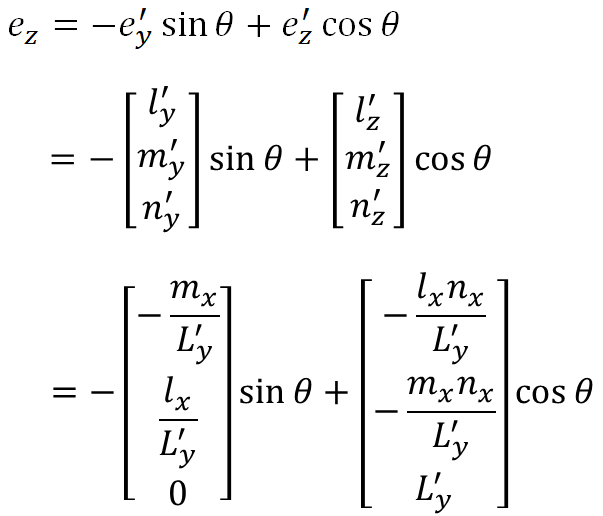
ここで、
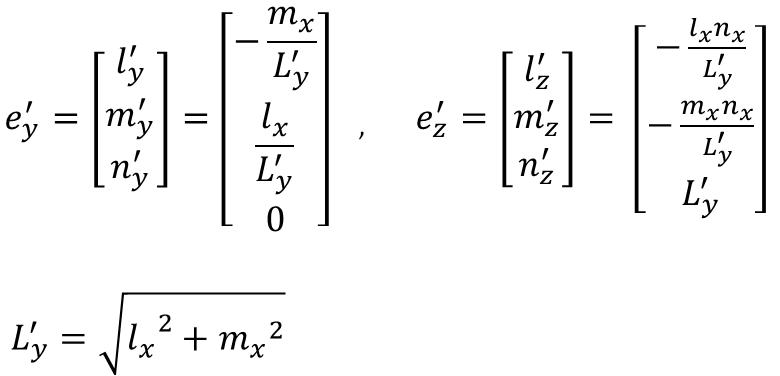
以上で、コードアングルを用いた方向余弦の式を全て導き出すことができました。
8.まとめ
最後に、全体座標系の座標(GX, GY, GZ)を、部材座標系の座標(x, y, z)に変換する座標変換マトリクスと、部材座標軸の全体座標軸に対する方向余弦を列記します。
(1) 座標変換マトリクス
全体座標系の座標(GX, GY, GZ)を、部材座標系の座標(x, y, z)に変換する座標変換マトリクスです。
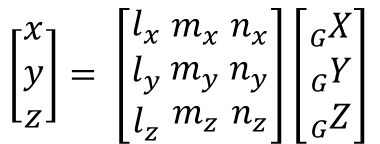
(2) 部材座標系x軸の全体座標軸に対する方向余弦

(3) 部材座標系y軸の全体座標軸に対する方向余弦
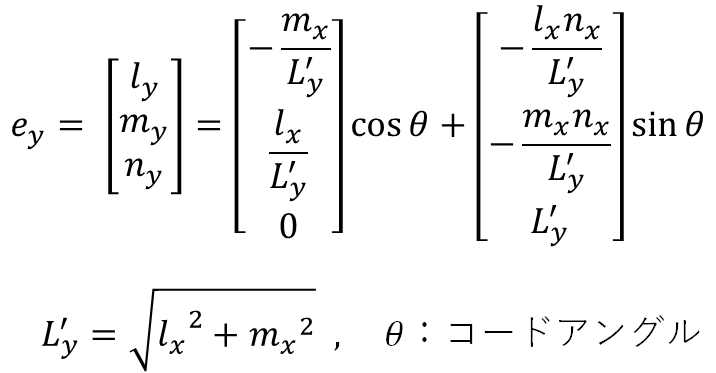
(3) 部材座標系z軸の全体座標軸に対する方向余弦
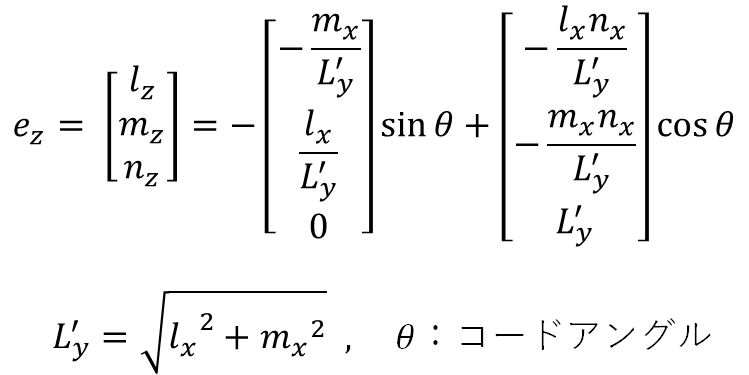
以上、方向余弦の結果だけ必要な場合に参照してください。
私が実際に購入した教材のご紹介
以下、私が実際に購入したPythonの教材をまとめてみました。 Pythonを学習する上で、少しでもお役に立つことができればうれしいです。
・Python♪私が購入したPythonの書籍のレビュー
・UdemyのPythonの動画講座を書籍を買う感覚で購入してみた
その他
液晶ペンタブレットを買いました
(1) モバイルディスプレイを買うつもりだったのに激安ペンタブレット購入
以下、私が光回線を導入した時の記事一覧です。
(1) 2020年「光回線は値段で選ぶ」では後悔する ←宅内工事の状況も説明しています。
(2) NURO光の開通までWiFiルーターを格安レンタルできる
(3) NURO光の屋外工事の状況をご紹介。その日に開通!
(4) 光回線開通!実測するとNURO光はやっぱり速かった
(5) ネット上のNURO光紹介特典は個人情報がもれないの?

