Python♪FEM：回転行列による座標やベクトルの回転

回転行列による座標やベクトルの回転について説明します。なお、回転では同じ座標を回転する場合と、座標系を回転させる場合で計算方法が変わります。図を見ながら「座標」「節点荷重ベクトル」「節点変位ベクトル」の座標変換について説明したいと思います。

０． FEMなど数値解析シリーズ
１．座標の回転
２．座標系の回転
３．節点座標を全体座標系から部材座標系へ
４．節点荷重ベクトルの座標変換
５．座標変換の例
６．おまけ（3次方程式の回転）
私が実際に購入した教材のご紹介
その他

０． FEMなど数値解析シリーズ

この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。

Python♪FEMなど数値解析シリーズ

１．座標の回転

座標(x0, y0)を反時計回りにθ(rad.)回転させた座標が(x1, y1)であるとき、(x0, y0)と(x1, y1)の関係を以下のような式で表すことができます。

なお、下の行列を回転行列といいます。この回転行列だけは必ず覚えましょう。回転の方向が反時計回りであることに注意する必要があります。

私は「反対に回る時計は、ここにはないさ」と覚えました。

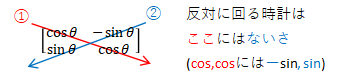
それでは、次に回転方向を逆にして、時計回りにθ(rad.)回転させてみましょう。上の回転行列の「θ」に「－θ」を代入すると下式を求めることができます。sinの前の符号が反時計回りの時と逆になります。

２．座標系の回転

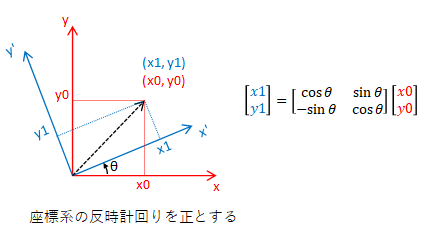
次は、座標系を反時計回りに回転させてみます。

下図で座標系（x-y）を座標系（x'-y'）に変換すると座標系は反時計回りであるのに対して、座標(x0,y0)は時計回りに回転します。

つまり、座標系を回転させることは、座標を逆回りに回転させることと同じことです。

３．節点座標を全体座標系から部材座標系へ

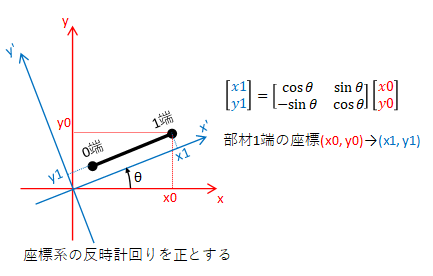
全体座標系を部材座標系に変換してみます。なお、部材座標系とはx'軸が部材と平行な座標系のことです。

下図の黒太線は部材です。部材の1端の座標は全体座標系では(x0, y0)、部材座標系では(x1, y1)です。座標系を反時計回りにθ(rad.)回転することで、全体座標系を部材座標系に変換できます。

しかし、実はFEMで威力を発揮するのは、節点座標の座標系を変換する時ではなく、節点荷重ベクトルや節点変位ベクトルの座標系を変換する時なのです。次はこれらについても考えてみましょう。

４．節点荷重ベクトルの座標変換

今度は部材の1端に節点荷重Pをかけました。節点荷重ベクトルは全体座標系では(x0, y0)です。この節点荷重ベクトルを部材座標系に変換すると、どのようになるのでしょうか。

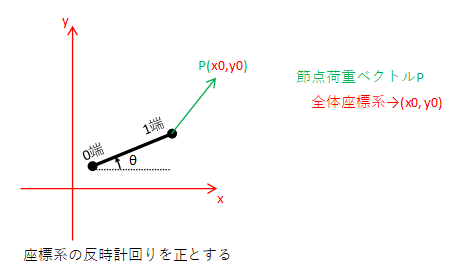
今までと同じように考えれば下の図のようになりますが、これではよくわかりません。節点荷重はベクトルですから、座標系の原点をベクトルの始点に合わせる必要があります。

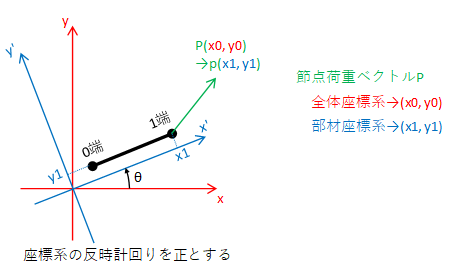
そこで、下図のように、節点荷重ベクトルの始点に座標系の原点を合わせれば、今までと同じ式を用いて節点荷重ベクトルを全体座標系から部材座標系に変換することができます。

部材座標系に変換すると節点荷重pを材軸方向の荷重x1と部材と直交方向の荷重y1に変換することができるので、荷重を部材の軸力とせん断力に分解することができます。また、トラスの場合は部材の両端がピンであるため、せん断力y1はゼロです。

この様に、荷重ベクトルの座標系を変換する計算はFEM解析において重要な計算です。

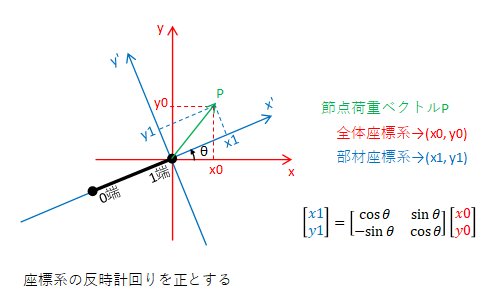
補足ですが、下の図は荷重ベクトルの始点に合わせる前の座標系も並記したものです。上の図と比較して理解しやすい方を参考にしてください。

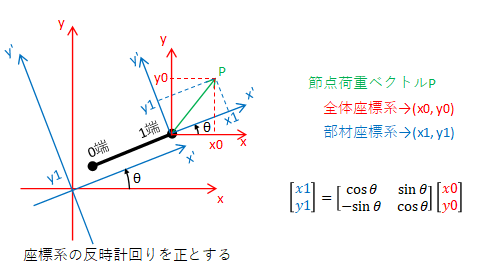
なお、節点変位ベクトルについても、節点荷重ベクトルと全く同様に考えることができます。

５．座標変換の例

もう少し、座標変換を自由自在に扱うために、いくつかの例を紹介します。

やり方を暗記するのではなく、座標を変換するマトリクス（座標変換マトリクス）をどの様に書き換えれば、自分の思ったような座標変換ができるのかを考えながら、行列の式を眺めてください。

(1) 2節点を同時に回転

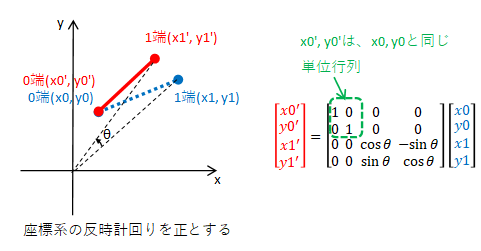
座標変換を行う節点が2つある場合の扱いについて考えてみます。原点を中心として、青い部材を反時計回りにθ(rad.)回転し、赤い部材の位置に移動します。

(x0', y0')は回転前の座標(x0, y0)とθだけ分かれば求めることができ、(x1, y1)は(x0', y0')の位置に影響を与えません。このように影響を与えない部分は下式の緑枠部分のように座標変換マトリクスの要素を0とします。

(x0, y0)→(x0', y0')や(x1, y1)→(x1', y1')の回転に関する部分は、お馴染みのsin,cosの式となっています。

(2) 2節点のうち1節点だけ回転

部材両側の2節点の内、1つだけ反時計回りにθ(rad.)回転する場合はどうでしょうか。この場合は、(x0,y0)=(x0', y0')なので、緑で囲んだ部分が単位行列（対角が1、それ以外は0）となっています。

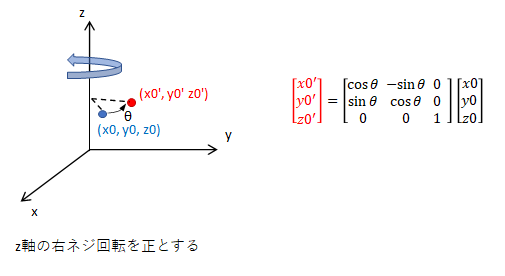
(3) 3次元座標のz軸回りの回転

3次元の座標において、z軸回りに回転する場合はz座標は変化しないので下式となります。このとき、z軸の右ネジ方向の回転を正とします。

６．おまけ（3次方程式の回転）

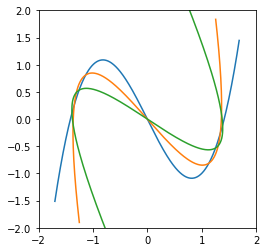
Pythonで以下の①～③の式を描画してみました。①は回転なし。②は行列は使わずsinθ,cosθを使って回転。③は座標変換マトリクス（回転行列）を使って回転しました。
　①「y = x ** 3 - 2 * x」（青）
　②「y = x ** 3 - 2 * x」を15度回転（黄）
　③「y = x ** 3 - 2 * x」を30度回転（緑）

行列の積はNumPyを使って計算します。49行目の「xy2 = np.dot(a, b)」が、行列aと行列bの積を求める部分です。

#コード01
# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
ax.set_xlim([-2, 2])   #x軸の範囲
ax.set_ylim([-2, 2])   #y軸の範囲
ax.set_aspect('equal') #グラフのアスペクト比を1:1

#y = x ** 3 - 2 * x
x0 = []
y0 = []
for i in range(-170, 170):
    x = i / 100
    y = x ** 3 - 2 * x
    x0.append(x)
    y0.append(y)
ax.plot(x0, y0)

#y = x ** 3 - 2 * x を15度回転
x1 = []
y1 = []
for i in range(-170, 170):
    x = i / 100
    y = x ** 3 - 2 * x
    theta = 15 * np.pi / 180  #degreeをradianに変換
    s = np.sin(theta)
    c = np.cos(theta)
    xx = c * x  - s * y
    yy = s * x  + c * y
    x1.append(xx)
    y1.append(yy)
ax.plot(x1, y1)

#y = x ** 3 - 2 * x を30度回転
x2 = []
y2 = []
for i in range(-170, 170):
    x = i / 100
    y = x ** 3 - 2 * x
    b = np.array([x, y])
    theta = 30 * np.pi / 180  #degreeをradianに変換
    s = np.sin(theta)
    c = np.cos(theta)
    a = [[c, -s]
        ,[s,  c]]
    xy2 = np.dot(a, b)  #aとbの積
    x2.append(xy2[0])
    y2.append(xy2[1])
ax.plot(x2, y2)

plt.show

座標変換の結果を図にすると楽しいですね。