立体フレームのFEMでコードアングルから方向余弦を求める式を求めるには、空間ベクトルの外積と内積を使います。内積はベクトルのなす角度や正射影ベクトルを求めることができます。また、外積は2つのベクトルに垂直なベクトルを求めることができます。
空間図形を扱うときには、内積や外積は強力なツールになりますので、ざっと復習してみたいと思います。
0. FEMなど数値解析シリーズ
この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。
1.空間ベクトルの内積
空間ベクトルの内積について、簡単に説明します。
(1) 内積の求め方
ベクトルa、ベクトルbの内積は以下の2種類の方法で求めることができます。
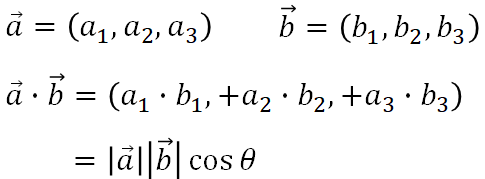
(2) ベクトルのなす角
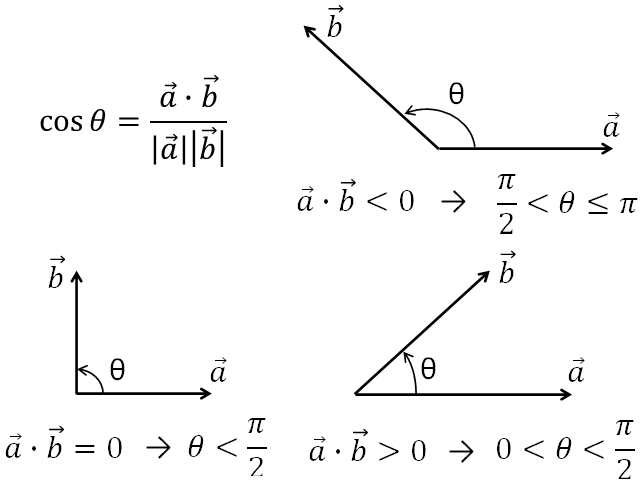
内積を用いることで、2つのベクトルのなす角をcosθの形で求めることができます。
また、内積=0の時にはθ=90度であり、内積の正負によって、θの大きさが90度よりも大きいか小さいかを判別できます。
(3) 正射影ベクトル
内積を使うことで、正射影ベクトルを求めることができます。ベクトルOHは、ベクトルbのベクトルaへの正射影ベクトルです。
立体フレームの方向余弦の算定では使いませんが、便利なので覚えておきましょう。

2.空間ベクトルの外積
空間ベクトルの外積について、簡単に説明します。
(1) 外積の求め方
外積は以下の方法で求めます。ただ、これでは式が複雑でなかなか覚えることができません。なお、内積は値でしたが、外積はベクトルです。
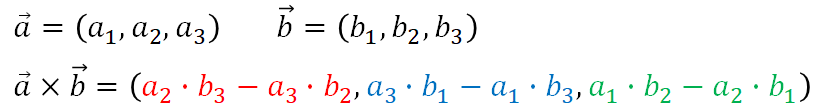
そこで、各ベクトルの要素をそれぞれ横に並べ、更にa1, b1を一つ追加した図を用意します。そして、下図の順番で、たすき掛けで差を求めます。上の式と下の図の色をそろえましたので、比較してください。
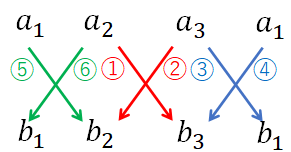
(2) 2つのベクトルに垂直なベクトル
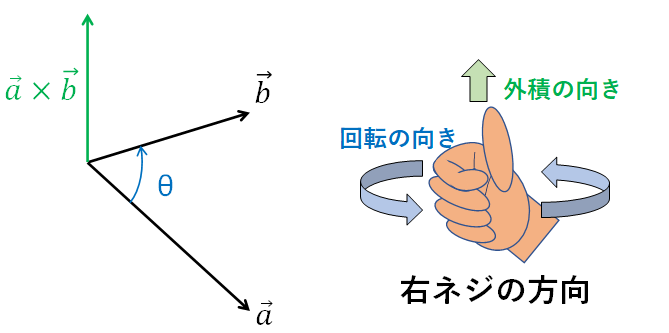
外積は2つのベクトルに垂直なベクトルです。これは大変便利な特徴ですので覚えておいてください。また、ベクトルaからベクトルbの方向を右ねじの回転の正方向とすると、外積の向きを求めることができます。
(3) 2平面の交線のベクトル
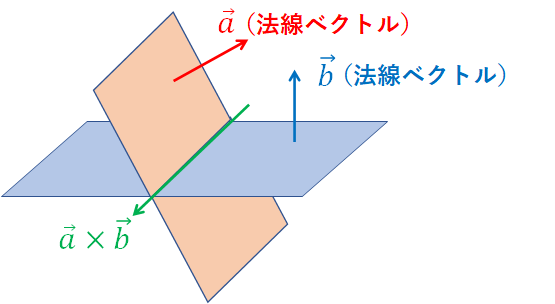
外積が2つのベクトルに垂直なベクトルであることを応用すると、2平面の交線の方向を示すベクトルを求めることができます。
2平面の交線は、2平面それぞれの法線ベクトルに垂直なベクトルでもあります。
(4) 外積の長さ
外積の長さは、ベクトルの要素から求めることができますが、sinθを使って求めることができます。また、外積の長さは下図のように平行四辺形の面積に等しいです。
つまり、直行する単位ベクトルの外積は1辺の長さが1の正方形の面積を求めることに等しいので、外積は単位ベクトルになります。
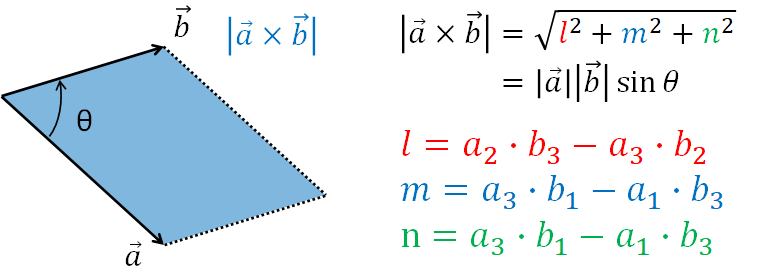
私が実際に購入した教材のご紹介
以下、私が実際に購入したPythonの教材をまとめてみました。 Pythonを学習する上で、少しでもお役に立つことができればうれしいです。
・Python♪私が購入したPythonの書籍のレビュー
・UdemyのPythonの動画講座を書籍を買う感覚で購入してみた
その他
液晶ペンタブレットを買いました
(1) モバイルディスプレイを買うつもりだったのに激安ペンタブレット購入
以下、私が光回線を導入した時の記事一覧です。
(1) 2020年「光回線は値段で選ぶ」では後悔する ←宅内工事の状況も説明しています。
(2) NURO光の開通までWiFiルーターを格安レンタルできる
(3) NURO光の屋外工事の状況をご紹介。その日に開通!
(4) 光回線開通!実測するとNURO光はやっぱり速かった
(5) ネット上のNURO光紹介特典は個人情報がもれないの?

