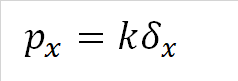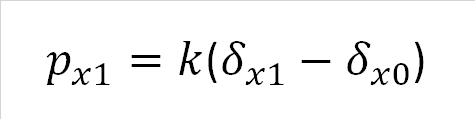Python♪FEM:部材座標系の要素剛性マトリクス

バネの式は中学生に習いますが、これを行列で表現すると聞くと急に難しく感じてしまいます。でも、順を追って理解すれば難しいものではありません。Ｆ＝ｋ・xの式から要素剛性マトリクスを求めるまでの過程を説明したいと思います。

０． FEMなど数値解析シリーズ
１．軸力とバネの伸びの関係
２．外力と両側の節点変位の関係
３．要素剛性マトリクス（軸方向のみ）
- (1) 要素剛性マトリクス
- (2) 例題1
４．要素剛性マトリクス（部材直交方向考慮）
５．次のステップへの導入
６．トラス解析プログラムの全体の流れ
私が実際に購入した教材のご紹介
その他

０． FEMなど数値解析シリーズ

この記事は「FEMなど数値解析シリーズ」の記事です。一連の記事は、以下のリンク集を参照してください。

１．軸力とバネの伸びの関係

下図は部材の左側が固定されていて、右側の節点に右向きの力pxを加えた図です。そして載荷後の部材の伸びを変位δx、ばね定数をk とすると、pxとδxの関係は式(1-1)となります。また、ばね定数kは式(1-2)で求められるので、式(1-1)は式(1-3)に変形できます。

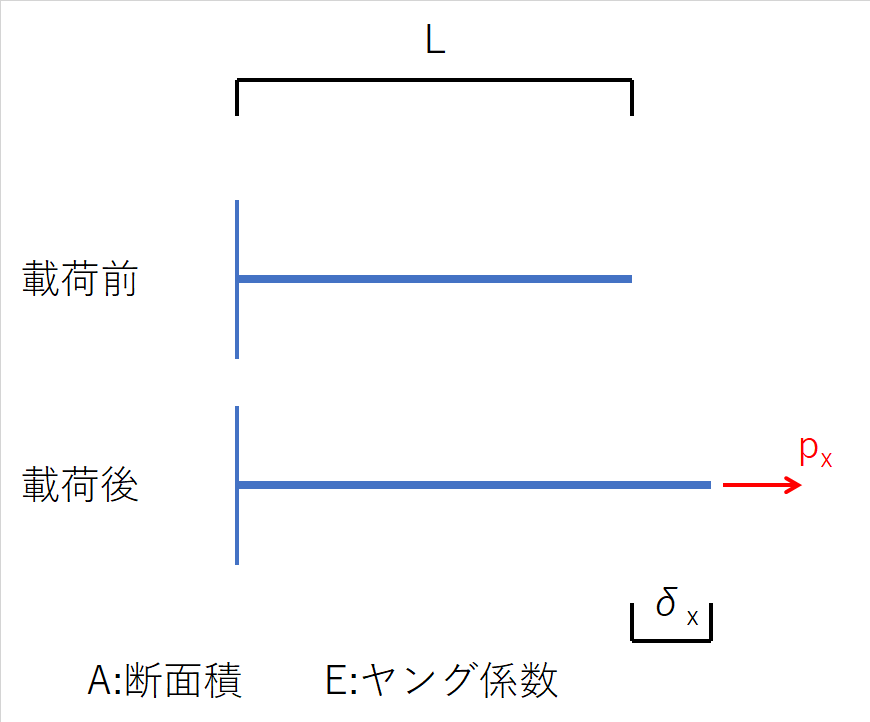
　　図 - 1　外力と伸びの関係

	式(1-1)
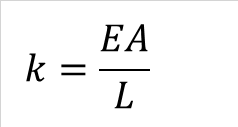	式(1-2)
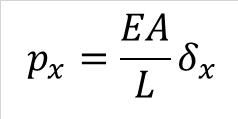	式(1-3)

２．外力と両側の節点変位の関係

次に下図のように２本の部材を直列につないだ構造の部材bだけに注目してみます。部材bの節点1に外力px1を加えると、節点0は右にδx0、節点1は右にδx1変位しました。この時、部材bの伸びは(δx1-δx0)となるので、式(2)を求めることができます。なお、節点0側の反力は右向きが正ならば-px1となります。

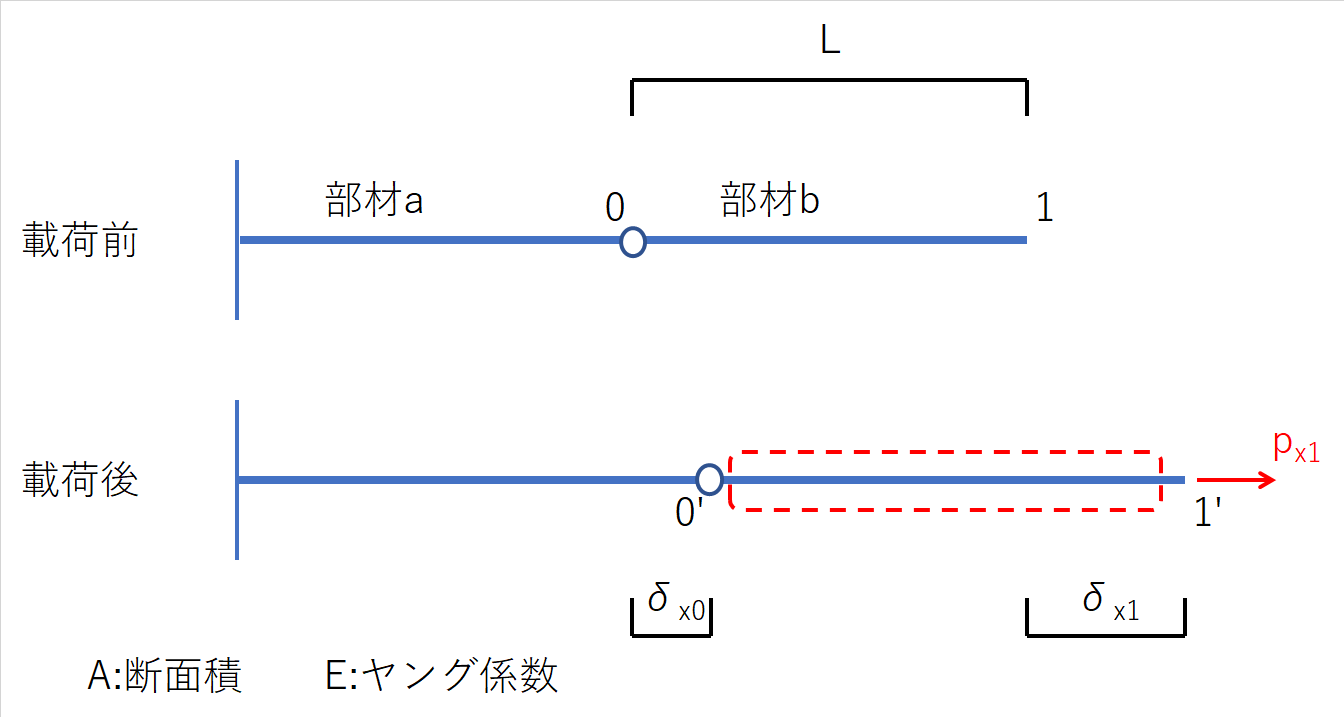
　　　図-２　部材外力と部材両端変位の関係

式(2)

３．要素剛性マトリクス（軸方向のみ）

それでは、いよいよ部材外力と節点変位の関係を行列で表現します。

(1) 要素剛性マトリクス

下図は図-2の部材bを節点のすぐ内側で切り出したものです。なお、節点変位も外力もすべて右向きが正です。

すると、外力と変位の関係は式(3-1)、式(3-2)となります。式(3-1)は節点0の外力px0と部材両端の節点変位δx0、δx1の関係を示す式であり、式(3-2)は節点1の外力px1と部材両端の節点変位δx0、δx1の関係を示す式です。

そして、式(3-1)と式(3-2)を行列を使った式で表したものが式(3-3)です。しっかりと式を見比べて、同じ内容の式であることを理解しましょう。式(3-1)、式(3-2）の赤色の部分が式(3-3)の剛性を表す行列に対応していることがわかります。

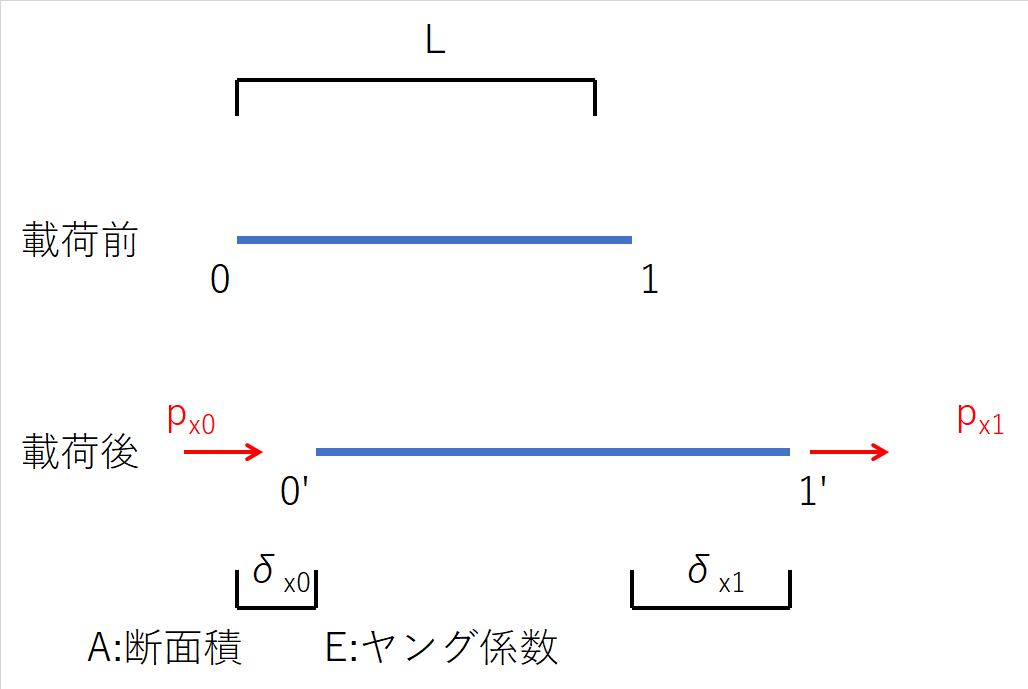
　　図-3-1　外力と節点変位の関係

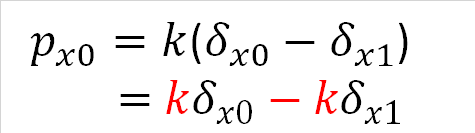	式(3-1)
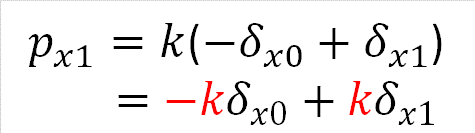	式(3-2)
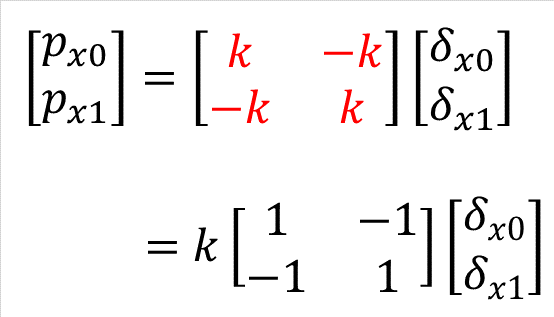	式(3-3)

なお、以下の式(3-4)の部分を「剛性マトリクス」といい、特に単一の部材要素の剛性マトリクスなので「要素剛性マトリクス」と呼びます。そして、式(3-3)を「要素剛性方程式」と呼びます。

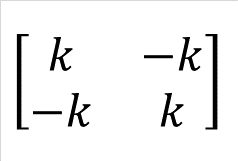式(3-4)

コンピューターは繰り返し計算と条件分岐を用いて行列計算を行うのが得意です。FEMのプログラミングでは、このように計算内容を行列の表現に置き換えることから始まります。

(2) 例題1

では、さっそく、上記の図-3-1において、δx0 = 1、δx1 = 2である場合の外力を求めてみましょう。

これは式(3-3)にδx0 = 1、δx1 = 2を代入し、以下、式(3 - 5)のように外力px1、 px2を求めることができます。

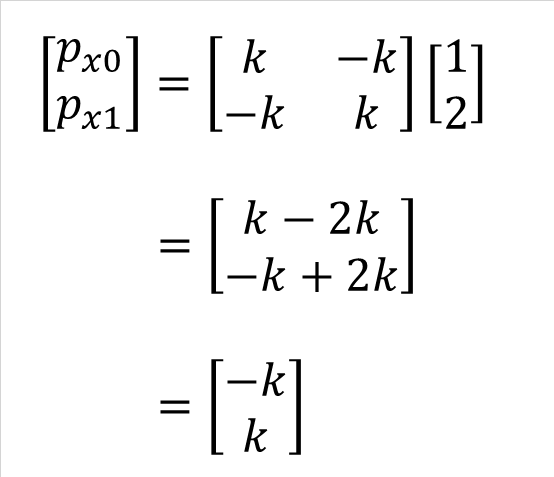式(3-5)

節点変位、外力ともに右側が正方向とすると、節点0の外力は-kなので節点1と大きさが同じで逆方向の外力になることがわかります。

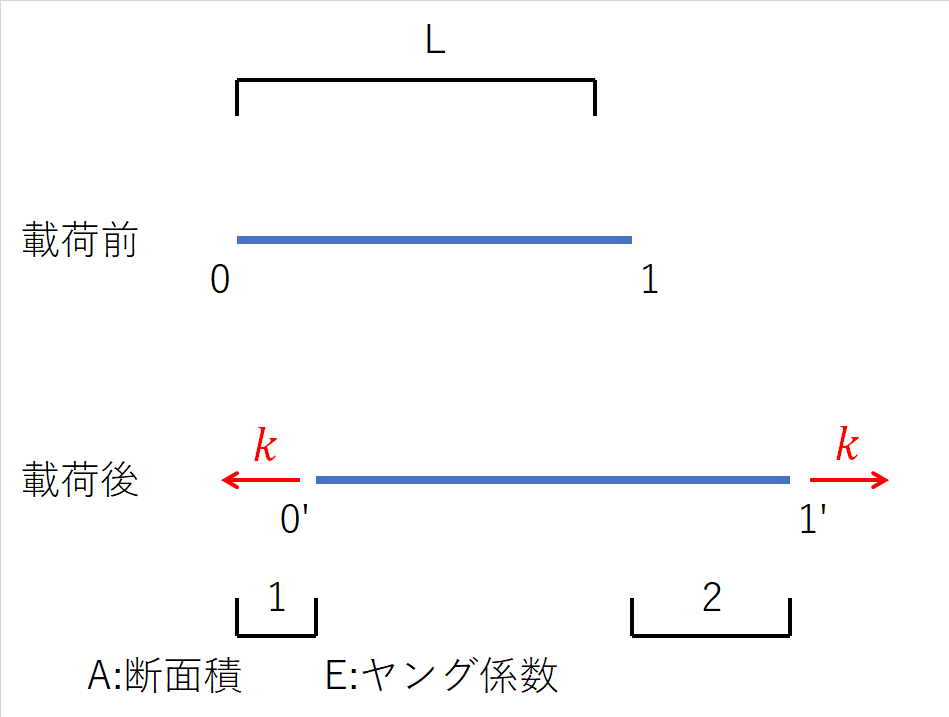
　　図-3-2　変位から外力を求める

４．要素剛性マトリクス（部材直交方向考慮）

式(3-4)の要素剛性マトリクスは材軸方向のみを考慮したものですが、部材と直交方向の外力や節点変位を考慮した要素剛性マトリクスを求めることもできます。

下図に外力と節点変位の関係を示します。部材の材軸方向をx方向とし、部材に直交する方向をy方向とします。部材が構造物のなかでどのような向きに配置されていたとしても、部材の材軸方向をx方向とし、このような座標系を「部材座標系」と呼びます。

部材節点への外力はpx0、py0、px1、py1であり、載荷後の節点変位はδx0、δy0、δx1、δy1です。

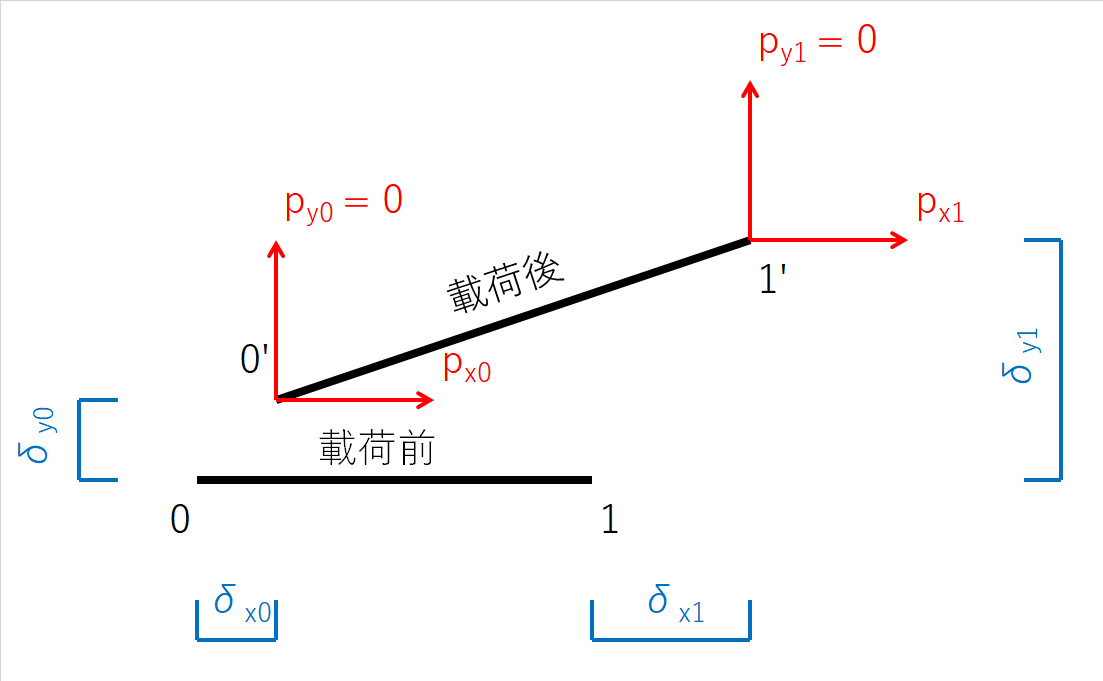
　図-4　外力と変位の関係（部材直交方向考慮）

式(4-1)は節点0のx方向の外力を求める式です。材軸方向のみ考慮した式(3-1)と比較し、0・δy0、0・δy1の項が加わっています。部材に直交するy方向の変位は部材軸力に影響を与えないので、どんな値が代入されたとしても外力px0を求める計算に与える影響が0であることを示します。

式(4-2)は節点0のy方向の外力を求める式です。トラス部材は部材に直交する方向には抵抗しないため、部材両端の節点が直交方向にどれだけ変位したとしても、py0はゼロです。つまり、δx0、δy0、δx1、δy1の係数をすべてゼロにすることにより、どんな値を代入してもpy0がゼロになります。

なお、py0がゼロになる理由がわからない場合には、以下の記事を読み直してください。「微小変形」の考え方を復習するとすっきりします。

FEM:微小変形の仮定と人の感覚の違い

また、同様の考え方で式(4-3)、式(4-4)を求めます。

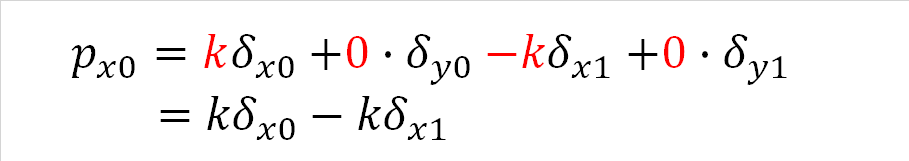	式(4-1)
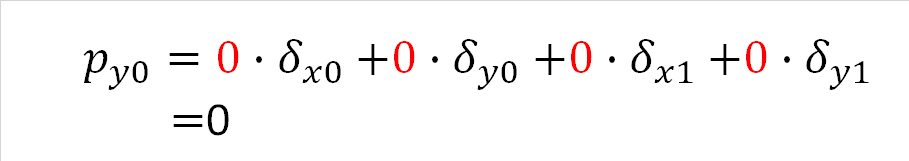	式(4-2)
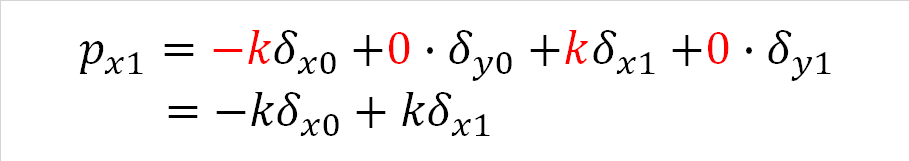	式(4-3)
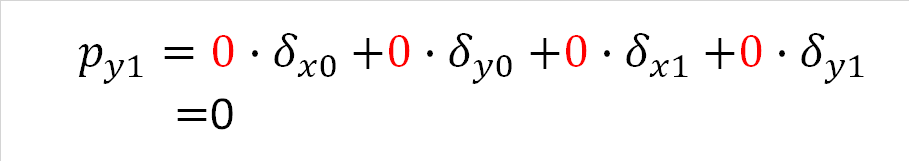	式(4-4)

式(4-1)～(4-4)から行列を使った要素剛性方程式を求めたものが式(4-5)です。式(4-1)～式(4-4)の赤色の係数部分が要素剛性マトリクスに対応していることがわかります。

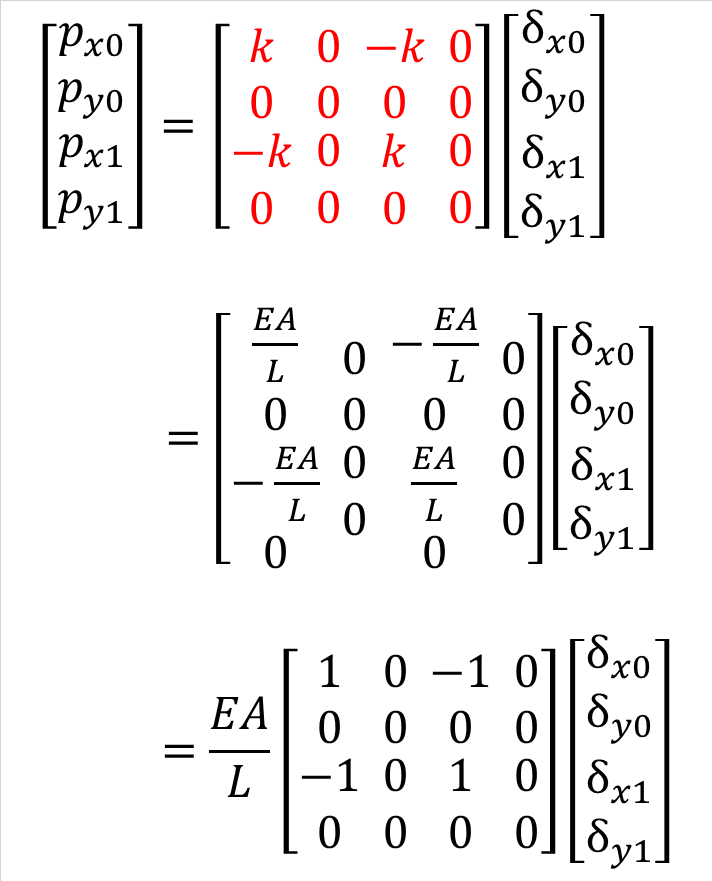式(4-5)

手計算では係数が全て0になる式は考えませんし、無意味な式であるように感じるかもしれません。しかし、様々な方向の部材を組み合わせた構造物を計算では、ある特定の変位が力の釣り合いに影響を与えないという情報は重要な情報です。

なお、FEMのプログラムでは軸方向のみを考慮した式(3-3)を使っても、直交方向を考慮した式(4-5)を使ってもコードを記述することができます。ただ、式(3-3)を使う場合はこれらの情報が要素剛性方程式に含まれていないので、コードの記述を工夫する必要があります。

いかがでしょうか。これで、部材座標系の要素剛性マトリクスの説明は終了です。微小変形の考え方が理解できていれば、それほど難しくないのではないでしょうか。

５．次のステップへの導入

それでは、次のステップへの導入として、もう一度、図-3-1と式(3-3)を見てみましょう。例題1ではδx0=1、δx1=2からpx0、px1を求めましたが、今度は逆にpx0 = -2、px1 = 2から節点変位を求めてみましょう。

なお、実際の計算では今度の例のように荷重から構造物の変形を求めることがほとんどだと思いますので、例題1よりも実践に近い問題です。

　　図-3-1　外力と節点変位の関係

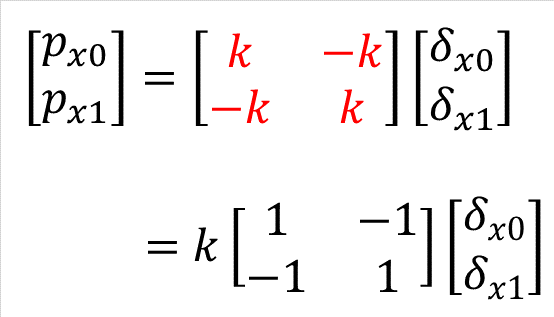式(3-3)

px0=-2、px1=2を式(3-3)に代入すると式(5-1)になり、解は式(5-2)となります。しかし、式(5-2)の逆行列の部分は計算ができません。

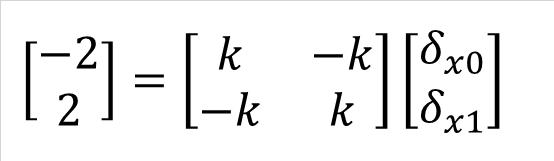	式(5-1)
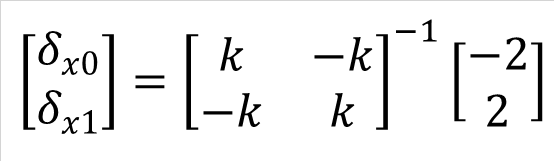	式(5-2)

式(5-3)は2行2列の行列の逆行列を求める式です。式(5-2)をこの求め方で解こうとすると、ad - bcの部分がk×k - (-k)×(-k) = 0となり、逆行列を求めることができないのです。

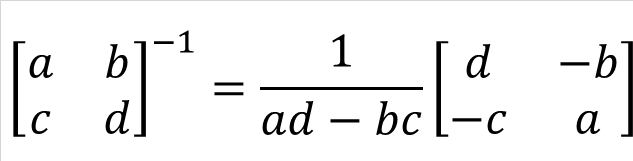式(5-3)

しかし、よく考えると当然のことです。例えば部材軸力が例題1でδx0=1、δx1=2の場合の部材軸力はkになりますが、逆に部材軸力がkとなる変位は、δx1とδx0の差が1になればよいため「δx0=2、δx1=3」も「δx0=5、δx1=6」も解になり、解が１つには定まらないのです。

「これじゃ、要素剛性マトリクスって組む意味あるの？」と思うかもしれませんが、心配いりません。実際の構造物は図3-1のように空中に浮いているわけではないからです。

例えば下の構造物では、部材左側の部分の変位がゼロであるという境界条件が条件として追加されます。

また、部材を直列に並べた構造物では、下図の部材bだけではδx0、δx1を求めることはできませんが、各部材の要素剛性マトリクスを組み合わせて部材全体の剛性マトリクスを作ることで解を求めることができます。なお、複数の部材を組み合わせるときには、それぞれの部材でバラバラの部材座標系を同一の座標系に変換する必要があります。